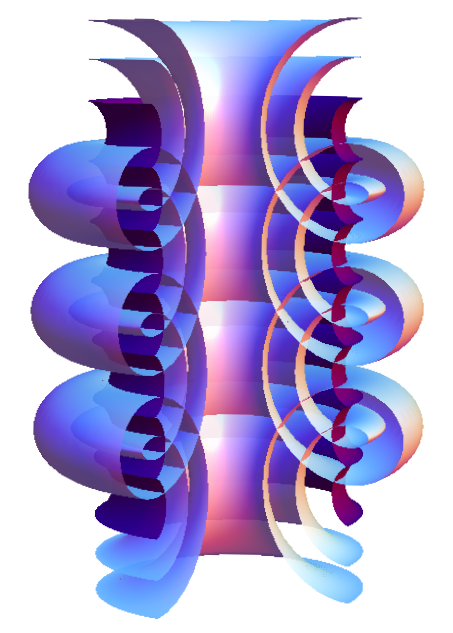
 Channel linear Weingarten surfaces
Channel linear Weingarten surfaces
(Fig: K Mundilova)
|
Abstract.
Properties or equations used to
specify geometric objects possess certain symmetries, such as the
specification of a triangle in terms of three angles, which determines
a triangle up to similarity, or in terms of three edge lengths, which
determines it up to Euclidean motion: these two specifications have
different symmetry groups. Various theorems in geometry describe a
situation, whereby a "conserved quantity",
naturally associated with a geometric object, reduces the symmetry
group of its defining properties:
the original symmetry is broken.
Vessiot's theorem yields a classical example of symmetry breaking in
differential geometry: if a surface can be deformed while preserving
all properties relating to angle measurement and, at the same time,
envelops a 1-parameter family of spheres, then it is piece of a cone,
a cylinder or a surface of revolution. The first two properties only
depend on an angle measurement, while being a cone, cylinder or
surface of revolution depends on a length measurement.
Thus symmetry breaking has occurred.
We will investigate relations between non-rigidity and symmetry
breaking, in particular, whether deformability in more than one way
invariably leads to symmetry breaking, thus generalizing Vessiot's
theorem. However, our main concern will be to detect
causes for symmetry breaking
rather than just its occurrence, for example, by studying the
appearance of the aforementioned "conserved quantities".
|

 Technische Universität Wien
Technische Universität Wien