|
|
I1671-N26: Transformations and Singularities
Joint Project between Austria (FWF) and Japan (JSPS)
|
|


|
Project leader (Austria): Udo Hertrich-Jeromin
Project leader (Japan): Yoshihiko Suyama
Funding period (Austria): 1 Jul 2014 - 31 Mar 2018
(approved 14 Mar 2014)
Field: Mathematics;
Areas: Differential geometry, Singularity theory, Integrable
systems, Discrete differential geometry
|

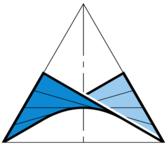
 Ellipsoid and Christoffel transform
Ellipsoid and Christoffel transform
with ends at the umbilics
|
Abstract.
Transformations of surfaces allow to construct new (families of)
surfaces of the same kind.
The concept of transformation is rather far-reaching:
for example, the Weierstrass representation of minimal surfaces
can be interpreted as a special case.
Moreover, discrete (facetted) surfaces of the same kind
naturally occur from repeated transformations.
Singularities are, most generally, the "bad points"
of a theory, points at which the methods of a theory fail.
This already constitutes a strong motivation for their study:
the employed methods require extension,
the studied objects reconsideration,
and new viewpoints on the theory arise.
The aim of this project is to study the interplay
between transformations and singularities.
More precisely:
we aim to
- understand how transformations of particular
surfaces behave (or fail to behave) at singularities;
and
- study how those transformations create (or annihilate)
singularities,
and what the nature of the occurring singularities is.
A good understanding of the interplay between transformations
and singularities will shed further light on either theory.
Moreover,
new results and phenomena will arise from this interplay,
for example,
regarding "singularities" of facetted or paneled
surfaces.
|
|
Publications.
- F Burstall, U Hertrich-Jeromin, C Müller, W Rossman (2016)
-
Semi-discrete isothermic surfaces;
Geom Dedicata 183, 43-58 (2016)
DOI:10.1007/s10711-016-0143-7
Abstract
A Darboux transformation for polarized space curves is
introduced and its properties are studied, in particular,
Bianchi permutability. Semi-discrete isothermic surfaces are
described as sequences of Darboux transforms of polarized
curves in the conformal $n$-sphere and their transformation
theory is studied. Semi-discrete surfaces of constant mean
curvature are studied as an application of the transformation
theory.
- A Honda (2016)
-
Weakly complete wave fronts with one principal curvature constant;
Kyushu J Math 70, 217-226 (2016)
DOI:10.2206/kyushujm.70.217
Abstract
Murata and Umehara gave a classification of complete
flat fronts in the Euclidean 3-space and proved their
orientability. Here, a flat front is a flat surface (i.e., a
surface where one of the principal curvatures is identically
zero) with admissible singularities. In this paper,we
investigate wave fronts where one of the principal curvatures
is a non-zero constant. Although they are orientable in the
regular surface case, there exist non-orientable examples. We
classify weakly complete ones and derive their orientability.
- V Branding, W Rossman (2017)
-
Magnetic geodesics on surfaces with singularities;
Pac J Math Ind 9, 3 (2017)
DOI:10.1186/s40736-017-0028-1
Abstract
We focus on the numerical study of magnetic geodesics on
surfaces, including surfaces with singularities. In addition
to the numerical investigation, we give restrictive necessary
conditions for tangency directions of magnetic geodesics
passing through certain types of singularities.
- W Carl (2017)
-
On semidiscrete constant mean curvature surfaces
and their associated families;
Monatsh Math 182, 537-563 (2017)
DOI:10.1007/s00605-016-0929-6
Abstract
The present paper studies semidiscrete surfaces in
three-dimensional Euclidean space within the framework
of integrable systems. In particular, we investigate
semidiscrete surfaces with constant mean curvature along
with their associated families. The notion of mean curvature
introduced in this paper is motivated by a recently developed
curvature theory for quadrilateral meshes equipped with unit
normal vectors at the vertices, and extends previous work
on semidiscrete surfaces. In the situation of vanishing
mean curvature, the associated families are defined via a
Weierstrass representation. For the general cmc case, we
introduce a Lax pair representation that directly defines
associated families of cmc surfaces, and is connected to a
semidiscrete sinh-Gordon equation. Utilizing this theory
we investigate semidiscrete Delaunay surfaces and their
connection to elliptic billiards.
- A Honda, M Koiso, M Kokubu, M Umehara, K Yamada (2017)
-
Mixed type surfaces with bounded mean curvature
in 3-dimensional space-times;
Differ Geom Appl 52, 64-77 (2017)
DOI:10.1016/j.difgeo.2017.03.009
Abstract
In this paper, we shall prove that space-like surfaces with
bounded mean curvature functions in real analytic Lorentzian
3-manifolds can change their causality to time-like surfaces
only if the mean curvature functions tend to zero. Moreover,
we shall show the existence of such surfaces with
non-vanishing mean curvature and investigate their properties.
- U Hertrich-Jeromin, A Honda (2017)
-
Minimal Darboux transformations;
Beitr Alg Geom 58, 81-91 (2017)
DOI:10.1007/s13366-016-0301-y,
EPrint arXiv:1602.06682
Abstract
We derive a permutability theorem for the Christoffel, Goursat
and Darboux transformations of isothermic surfaces. As a
consequence we obtain a simple proof of a relation between
Darboux pairs of minimal surfaces in Euclidean space, curved
flats in the 2-sphere and flat fronts in hyperbolic space.
- C Müller, M Yasumoto (2017)
-
Semi-discrete constant mean curvature surfaces of revolution
in Minkowski space;
in Mladenov, Meng, Yoshioka (eds),
Proc International Conference on Geometry, Integrability
and Quantization 18, 191-202 (2017)
DOI:10.7546/giq-18-2017-191-202
Abstract
In this paper we describe semi-discrete isothermic
constant mean curvature surfaces of revolution with smooth
profile curves in Minkowski three-space. Unlike the case of
semi-discrete constant mean curvature sur- faces in Euclidean
three-space, they might have certain types of singularities
in a sense defined by the second author in a previous work. We
analyze the singularities of such surfaces.
- Y Ogata, M Yasumoto (2017)
-
Construction of discrete constant mean curvature surfaces
in Riemannian spaceforms and applications;
Differ Geom Appl 54, 264-281
DOI:10.1016/j.difgeo.2017.04.010
Abstract
In this paper we give a construction for discrete constant
mean curvature surfaces in Riemannian spaceforms in terms of
integrable systems techniques, which we call the discrete DPW
method for discrete constant mean curvature surfaces. Using
this construction, we give several examples, and analyze
singularities of the parallel constant Gaussian curvature
surfaces.
- F Burstall, U Hertrich-Jeromin, W Rossman (2018)
-
Discrete linear Weingarten surfaces;
Nagoya Mathematical Journal 231, 55-88 (2018)
DOI:10.1017/nmj.2017.11
Abstract
Discrete linear Weingarten surfaces in space forms are
characterized as special discrete $\Omega$-nets, a discrete
analogue of Demoulin's $\Omega$-surfaces. It is shown that
the Lie-geometric deformation of $\Omega$-nets descends to a
Lawson transformation for discrete linear Weingarten surfaces,
which coincides with the well-known Lawson correspondence
in the constant mean curvature case.
- F Burstall, U Hertrich-Jeromin, Y Suyama (2018)
-
Curvilinear coordinates on generic conformally flat hypersurfaces
and constant curvature 2-metrics;
J Math Soc Japan 70(2), 617-649 (2018);
DOI:10.2969/jmsj/07027420
Abstract
There is a one-to-one correspondence between associated
families of generic conformally flat (local-)hypersurfaces in
$4$-dimensional space forms and conformally flat $3$-metrics with
the Guichard condition. In this paper, we study the space
of conformally flat $3$-metrics with the Guichard condition:
for a conformally flat $3$-metric with the Guichard condition
in the interior of the space, an evolution of orthogonal
(local-)Riemannian $2$-metrics with constant Gauss curvature
$-1$ is determined; for a $2$-metric belonging to a certain
class of orthogonal analytic $2$-metrics with constant Gauss
curvature $-1$, a one-parameter family of conformally flat
$3$-metrics with the Guichard condition is determined as
evolutions issuing from the $2$-metric.
- S Fujimori, U Hertrich-Jeromin, M Kokubu, M Umehara, K Yamada (2018)
-
Quadrics and Scherk towers;
Monatsh Math 186, 249-279 (2018)
DOI:10.1007/s00605-017-1075-5
Abstract
We investigate the relation between quadrics and their
Christoffel duals on the one hand, and certain zero mean
curvature surfaces and their Gauss maps on the other hand. To
study the relation between timelike minimal surfaces and the
Christoffel duals of 1-sheeted hyperboloids we introduce
para-holomorphic elliptic functions. The curves of type
change for real isothermic surfaces of mixed causal type
turn out to be aligned with the real curvature line net.
- S Fujimori (2018)
-
Triply periodic zero mean curvature surfaces in Lorentz-Minkowski 3-space;
Adv Stud Pure Math 78, 201-219 (2018)
DOI:10.2969/aspm/07810201
Abstract
We construct triply periodic zero mean curvature surfaces of
mixed type in the Lorentz-Minkowski 3-space $\mathbb{L}^3$,
with the same topology as the triply periodic minimal
surfaces in the Euclidean 3-space $\mathbb{R}^3$, called
Schwarz rPD surfaces.
- M Pember, G Szewieczek (2018)
-
Channel surfaces in Lie sphere geometry;
Beitr Algebra Geom 59, 779-796 (2018)
DOI:10.1007/s13366-018-0394-6
Abstract
We discuss channel surfaces in the context of Lie
sphere geometry and characterise them as certain
$\Omega_0$-surfaces. Since $\Omega_0$-surfaces possess
a rich transformation theory, we study the behaviour of
channel surfaces under these transformations. Furthermore,
by using certain Dupin cyclide congruences, we characterise
Ribaucour pairs of channel surfaces.
- F Burstall, U Hertrich-Jeromin, M Pember, W Rossman (2019)
-
Polynomial conserved quantities of Lie applicable surfaces;
manuscripta math 158, 505-546 (2019)
DOI:10.1007/s00229-018-1033-0
Abstract
Using the gauge theoretic approach for Lie applicable
surfaces, we characterise certain subclasses of surfaces
in terms of polynomial conserved quantities. These include
isothermic and Guichard surfaces of conformal geometry and
L-isothermic surfaces of Laguerre geometry. In this setting
one can see that the well known transformations available
for these surfaces are induced by the transformations of
the underlying Lie applicable surfaces. We also consider
linear Weingarten surfaces in this setting and develop a
new Bäcklund-type transformation for these surfaces.
- A Fuchs (2019 PhD thesis)
-
Transformations and singularities of isothermic surfaces;
PhD thesis, TU Wien (2019)
Abstract
We determine the limiting behaviour of Darboux and Calapso
transforms of polarized curves, where the polarization has
a pole of first or second order. We then study the analogous
problem for isothermic surfaces. We consider those isothermic
surfaces for which their Hopf differential factorizes into a
real function and a meromorphic quadratic differential. Upon
restriction to a simply connected patch, away from the zeros
and poles of this differential, the Darboux and Calapso
transformations yield new isothermic surfaces. We investigate
the limiting behaviour of these transformed patches as the
zeros and poles of the meromorphic quadratic differential
are approached and determine whether they are continuous
around those points.
- A Fuchs (2019)
-
Transformations and singularities of polarized curves;
Ann Glob Anal Geom 55, 529-553 (2019)
DOI:10.1007/s10455-018-9639-8
Abstract
We study the limiting behaviour of Darboux and
Calapso transforms of polarized curves in the conformal
$n$-dimensional sphere when the polarization has a pole of
first or second order at some point. We prove that for a
pole of first order, as the singularity is approached, all
Darboux transforms converge to the original curve and all
Calapso transforms converge. For a pole of second order,
a generic Darboux transform converges to the original
curve while a Calapso transform has a limit point or a
limit circle, depending on the value of the transformation
parameter. In particular, our results apply to Darboux and
Calapso transforms of isothermic surfaces when a singular
umbilic with index $1\over 2}$ or $1$ is approached along
a curvature line.
- U Hertrich-Jeromin, W Rossman, G Szewieczek (2020)
-
Discrete channel surfaces;
Math Z 294, 747-767 (2020)
DOI:10.1007/s00209-019-02389-4
Abstract
We present a definition of discrete channel surfaces in Lie
sphere geometry, which reflects several properties for smooth
channel surfaces. Various sets of data, defined at vertices,
on edges or on faces, are associated with a discrete channel
surface that may be used to reconstruct the underlying
particular discrete Legendre map. As an application we
investigate isothermic discrete channel surfaces and prove
a discrete version of Vessiot's Theorem.
- G Szewieczek (2021)
-
A duality for Guichard nets;
manuscripta math 164, 193-221 (2021)
https://doi.org/10.1007/s00229-020-01181-7
ti
so
DOI:10.1007/s00229-020-01181-7
Abstract
In this paper we study G-surfaces, a rather unknown surface
class originally defined by Calapso, and show that the
coordinate surfaces of a Guichard net are G-surfaces. Based
on this observation, we present distinguished Combescure
transformations that provide a duality for Guichard
nets. Another class of special Combescure transformations
is then used to construct a Bäcklund-type transformation
for Guichard nets. In this realm a permutability theorem
for the dual systems is proven.
|
|
Activities
Opening workshop
Vienna 15-20 Sep 2014
Closing workshop
Toyko 19-23 Feb 2016
People
Birgit Slama (Secretary)
Volker Branding (AT)
Wolfgang Carl (AT)
Andreas Fuchs (AT)
Shoichi Fujimori (JP)
Udo Hertrich-Jeromin (AT)
Atsufumi Honda (JP)
Satoshi Kawakubo (JP)
Masatoshi Kokubu (JP)
Nozomu Matsuura (JP)
Christian Müller (AT)
Kosuke Naokawa (JP)
Wayne Rossman (JP)
Yoshihiko Suyama (JP)
Gudrun Szewieczek (AT)
Masaaki Umehara (JP)
Johannes Wallner (AT)
Kotaro Yamada (JP)
Masashi Yasumoto (JP)
Links
FWF
- Austrian Science Fund
JSPS
- Japan Society for the Promotion of Science
TUW
- Vienna University of Technology
JASEC
- Japan-Austria Science Exchange Centre
DMG
- Institute of Discrete Mathematics and Geometry
|

 Technische Universität Wien
Technische Universität Wien