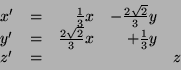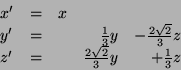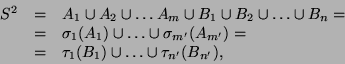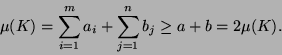Wie macht man 2 aus 1?
Das Paradoxon von Banach-Tarski
Reinhard Winkler,
TU Wien,
Österreichische Akademie der Wissenschaften
20.4.2001
pdf-version dieses Textes
Zusammenfassung:
Das vielleicht verblüffendste Ergebnis der modernen, auf der Mengenlehre
basierenden Mathematik ist das Paradoxon von Banach-Tarski.
Es erklärt, wie eine Kugel in Teile zerlegt werden kann,
welche - anders zusammengesetzt - zwei volle Kugeln ergeben, jede
gleich groß wie die ursprüngliche.
Der scheinbare Widerspruch zur Tatsache, dass durch Bewegungen keine
Volumina verändert werden können, löst sich auf, wenn man die
Konsequenz zieht, dass die Teile in der Zerlegung so kompliziert
sind, dass ihnen gar kein Volumen zugeordnet werden kann.
In diesem Artikel wird ein Beweis des Paradoxons von Banach-Tarski gebracht,
der sich zwar an Wagon's Monographie [Wa 2] anlehnt,
der aber kein mathematisches Wissen voraussetzt, das über den Schulstoff
noch vor der Infinitesimalrechnung hinausgeht.
Dementsprechend werden fundamentale Eigenschaften abzählbarer
und überabzählbarer Mengen, soweit sie für den Beweis notwendig sind,
im Text ausführlich besprochen. Die bei der Konstruktion der paradoxen
Zerlegung involvierten Drehungen werden ohne
Verwendung des Matrizenkalküls behandelt. Lediglich mit
linearen Gleichungssystemen wird umgegangen, deren Interpretation
als Drehungen explizit erläutert wird. Der Grenzwertbegriff
kommt nur implizit über die Zifferndarstellung reeller Zahlen vor.
Anschließend an den Beweis wird noch die Bedeutung des Paradoxons
in etwas größerem Kontext diskutiert. Solche Diskussionen über
die Bedeutung mathematischer Sätze in ideengeschichtlichem Zusammenhang
erscheinen für den Schulunterricht wünschenswert.
Der Artikel soll exemplarisch zeigen, dass es sehr wohl möglich
ist, anspruchsvolle Mathematik auf Schulniveau zu betreiben, ohne
sich in endlosen Rechnereien zu erschöpfen, und
dabei außerdem zu starken Resultaten zu gelangen,
ohne unzulässige Verkürzungen in Kauf nehmen zu müssen. Überdies können
anhand des Paradoxons von Banach-Tarski grundsätzliche Fragen über das
Wesen der Mathematik und anderer Wissenschaften angeschnitten werden.
1 Einführung
1.1 Worum geht es?
Grob gesprochen besagt das Paradoxon von Banach-Tarski (PvBT), dass es möglich
ist, eine Kugel in mehrere Teile zu zerlegen und diese so zusammenzusetzen,
dass man schlussendlich zwei Kugeln hat, von denen jede jeweils das gleiche
Volumen hat wie die ursprüngliche Kugel.
Diese Aussage klingt höchst paradox und scheint auf den ersten Blick
dem gesunden Menschenverstand zu widersprechen. Sie scheint nämlich
die Verdopplung von Volumina zu ermöglichen. Dieser scheinbare Widerspruch
löst sich auf, wenn man die Konsequenz zieht, dass die Kugelteile in
der Zerlegung ganz einfach kein wohldefiniertes Volumen besitzen,
weil sie so kompliziert sind, dass es zwar kaum vorstellbar aber
doch denkbar ist.
Zweifellos ist das Paradoxon von Banach-Tarski eines der spektakulärsten
Resultate der reinen Mathematik.
So sehr es auch zunächst verblüffen mag - nach etwas
eingehenderer Analyse verliert es seine (scheinbare) Absurdität und wird
zu einem ganz gewöhnlichen mathematischen Satz, der bewiesen und verstanden
werden kann.
Es zieht aber auch bedeutende innermathematische Konsequenzen nach sich und
gibt zu interessanten Überlegungen über das Verhältnis von Mathematik
und Wirklichkeit Anlass.
1.2 Die didaktischen Ambitionen dieses Artikels
Vorneweg soll betont werden, dass mündlicher Vortrag und schriftliche
Fixierung sehr unterschiedliche Mitteilungsformen sind, jede
mit Vor- und Nachteilen. Deshalb kann die vorliegende
schriftliche Fassung nicht dieselben Mittel einsetzen wie der
mündliche Vortrag.
Beiden Darstellungen gemeinsam ist der Versuch, durch sparsamen Einsatz
der mathematischen Zeichensprache den mit dieser nicht so
vertrauten Schüler, Leser oder Zuhörer nicht abzuschrecken. Anstelle
umfangreicher Formelketten
wird vor allem in der schriftlichen Fassung oft durch ausführliche
verbale Beschreibung ein anschaulicher Zugang zu den wichtigsten
Ideen angestrebt. Der mündliche Vortrag kann und soll
diesbezüglich einiges mit rhetorischen Mitteln ersetzen.
Das Wesen selbst mathematischer Beweise ist primär Überzeugungskraft
und nicht Formalisierung. Dennoch wird vor allem in der schriftlichen
Fassung der Anspruch auf Vollständigkeit der Beweise erhoben.
Das erste Hauptziel dieses Artikels, nämlich einen
kompletten Beweis einer Version des Paradoxons von Banach-Tarski
zu präsentieren, scheint angesichts der mathematischen Tiefe dieses
Satzes durchaus ehrgeizig. Schließlich handelt es sich bei den
Didaktikheften ja nicht primär um ein Forum für Fachartikel
aus der mathematischen Forschung. Es soll aber auch in didaktischem
Kontext kein Zweifel daran aufkommen, dass Beweise in der Mathematik
eine zentrale Rolle spielen. Natürlich wäre es verfehlt, Vollständigkeit
immer und überall zu fordern. Was mit angemessenem Aufwand verstehbar ist,
soll aber verstehbar gemacht werden. Die Akzeptanz
für Mathematik in der Öffentlichkeit kann sicher wesentlich verbessert
werden, wenn sich weniger Menschen ausgeschlossen fühlen.
Das Augenmerk wird im Beweis so sehr auf die wesentlichen
Ideen gelegt, dass das Resultat selbst für den mathematischen Laien plausibel,
für den nur durchschnittlich begabten und ambitionierten
Schüler oder Studienanfänger sogar restlos
verstehbar wird. Damit soll exemplarisch vorgeführt werden, dass sich
manche äußerst attraktive und bedeutende
Ergebnisse der Mathematik durchaus dafür eignen,
ohne Verkürzung einem deutlich breiteren Publikum zugänglich gemacht
zu werden, nicht nur Fachstudenten in fortgeschrittenen Semestern.
Insofern versteht sich dieser Artikel in erster Linie als didaktisch.
Hierin unterscheidet er sich nicht nur von den bald 100 Jahre
alten Originalarbeiten
[H] und [Ba-T], sondern auch von hervorragenden und leichter
lesbaren Artikeln jüngeren Datums wie [St] und [Wa 1].
In [Wa 2] liegt sogar eine sehr
empfehlenswerte Monographie zum Thema vor. Diese Werke richten sich
durchwegs an ein Publikum von, wenn auch nicht spezialisierten,
so doch mathematisch überdurchschnittlich ausgebildeten Lesern.
Das zweite Hauptziel des vorliegenden Artikels besteht darin,
wenigstens in Ansätzen die Bedeutung des Paradoxons von
Banach-Tarski im Gesamtkontext der Mathematik und sogar in darüber
hinausgehenden wissenschaftstheoretischen Zusammenhängen
zur Sprache zu bringen. Innermathematisch seien die Schlagworte wie Messbarkeit
von Mengen und Invarianz von Maßen bezüglich bestimmter Gruppen
von Transformationen erwähnt. Außermathematisch geht es z.B. um das Verhältnis zwischen Mathematik und empirischer Wirklichkeit
oder um generelle erkenntnistheoretische Fragen.
Der Relevanz von mathematischen oder anderen einzelwissenschaftlichen
Ergebnissen in größeren Zusammenhängen kann
im Unterricht kaum genug Bedeutung beigemessen werden.
Der Artikel richtet sich vor allem an Mathematiklehrer an Höheren Schulen
in der Hoffnung, dass das Gebotene reich genug ist, um eine individuelle
Auswahl für den Unterricht zu ermöglichen und Anregungen zu bieten.
In einer beliebigen Klasse der Oberstufe einer AHS sollten
geringfügige Anpassungen der Darstellung an den aktuellen Wissensstand
reichen, um den
präsentierten Stoff oder Teile davon im Unterricht einzubauen.
1.3 Eine exakte Formulierung des PvBT
Wir werden den vollständigen Beweis für das PvBT in folgender
Formulierung führen:
Das Paradoxon von Banach-Tarski:
Bezeichne  die volle Einheitskugel im dreidimensionalen Anschauungsraum.
(Formal ist das die Menge aller Punkte
die volle Einheitskugel im dreidimensionalen Anschauungsraum.
(Formal ist das die Menge aller Punkte
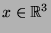 , deren Abstand
vom Koordinatenursprung nicht größer als eine Einheit ist.)
, deren Abstand
vom Koordinatenursprung nicht größer als eine Einheit ist.)
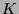 besitzt eine paradoxe Zerlegung bezüglich Bewegungen im
besitzt eine paradoxe Zerlegung bezüglich Bewegungen im
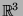 .
Das heißt:
.
Das heißt:
Es ist möglich, disjunkte (das heißt paarweise nicht überschneidende) Mengen
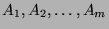 und
und
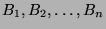 zu finden, welche zu zwei
vollen Kugeln, ebenfalls mit Radius 1, zusammengesetzt werden können.
Das soll wiederum bedeuten, dass es sogenannte Bewegungen (das sind
Transformationen, welche sich aus Drehungen und Schiebungen zusammensetzen)
zu finden, welche zu zwei
vollen Kugeln, ebenfalls mit Radius 1, zusammengesetzt werden können.
Das soll wiederum bedeuten, dass es sogenannte Bewegungen (das sind
Transformationen, welche sich aus Drehungen und Schiebungen zusammensetzen)
 ,
, 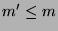 , und
, und
 ,
, 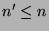 ,
gibt mit folgender Eigenschaft:
Unterwirft man die Mengen
,
gibt mit folgender Eigenschaft:
Unterwirft man die Mengen 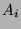 den
den  , so erhält man Mengen
, so erhält man Mengen 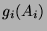 ,
deren Vereinigung die gesamte Kugel
,
deren Vereinigung die gesamte Kugel 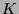 ergibt. Analoges gilt für die
ergibt. Analoges gilt für die
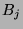 und
und 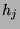 , also:
, also:
1.4 Mögliche Verschärfungen
Man beachte, dass in der obigen Formulierung des PvBT nicht
alle 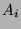 und
und 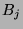 weiterverwendet werden, falls
weiterverwendet werden, falls 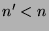 oder
oder 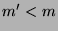 .
Man kann aber zeigen, dass
.
Man kann aber zeigen, dass 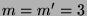 und
und 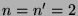 gewählt,
die Zerlegung also mit 5 Teilen bewerkstelligt werden kann.
Es gilt sogar die Verschärfung, dass je zwei beschränkte
Teilmengen des
gewählt,
die Zerlegung also mit 5 Teilen bewerkstelligt werden kann.
Es gilt sogar die Verschärfung, dass je zwei beschränkte
Teilmengen des
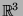 , welche beide irgendeine Kugel mit positivem Radius
enthalten, zerlegungsgleich sind. Das soll heißen, dass
man die eine Menge geeignet in endlich viele Stücke zerlegen kann die,
richtig zusammengesetzt, die andere Menge ergeben.
, welche beide irgendeine Kugel mit positivem Radius
enthalten, zerlegungsgleich sind. Das soll heißen, dass
man die eine Menge geeignet in endlich viele Stücke zerlegen kann die,
richtig zusammengesetzt, die andere Menge ergeben.
Der Beweis dieser Aussagen erfordert aber die Entwicklung umfangreicherer
Theorien oder technische Feinarbeit,
welche den Rahmen dieses Artikels sprengen oder gar
vom Kern des PvBT ablenken könnten. Als diesen Kern wollen wir die
Tatsache betrachten, dass aus Bestandteilen einer einzigen Kugel durch
geeignete Zusammensetzung zwei Kugeln entstehen können.
1.5 Überblick über die folgenden Kapitel
In Kapitel 2 werden einige klassische und als
Paradoxien des Unendlichen bekannte Beobachtungen erwähnt,
welche beispielsweise schon von Galilei [Ga] und Bolzano [Bo]
angestellt wurden. Sie liegen gedanklich exakt auf dem Weg zum PvBT
und können im Beweis erfolgreich eingesetzt werden. Außerdem werden fundamentale
Eigenschaften abzählbarer und überabzählbarer Mengen
wiederholt. Wer mit den grundlegenden Tatsache wie
Abzählbarkeit von 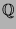 und Überabzählbarkeit von
und Überabzählbarkeit von 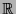 vertraut ist,
wird über die ersten Abschnitte rasch hinweggehen. Dennoch bilden sie
insbesondere ab 2.10 eine gezielte Vorbereitung auf das
Nachfolgende. Wer mehr wissen möchte, sei auf den ebenfalls in den Didaktikheften
erschienenen Artikel [Go] verwiesen, der ganz der
Mengenlehre gewidmet ist.
vertraut ist,
wird über die ersten Abschnitte rasch hinweggehen. Dennoch bilden sie
insbesondere ab 2.10 eine gezielte Vorbereitung auf das
Nachfolgende. Wer mehr wissen möchte, sei auf den ebenfalls in den Didaktikheften
erschienenen Artikel [Go] verwiesen, der ganz der
Mengenlehre gewidmet ist.
Kapitel 3 präsentiert den vollständigen Beweis des PvBT
in der Formulierung von 1.3.
Der wesentliche Durchbruch wurde 1914 von Hausdorff erzielt, siehe [H],
indem er eine paradoxe Zerlegung der Sphäre (Oberfläche der Kugel),
vermindert um eine abzählbare Menge, fand (vgl. 3.1).
Der entscheidende Schritt besteht erstens
in der zwar unanschaulichen aber trivial nachzuprüfenden Tatsache,
dass die von zwei Elementen frei erzeugte Gruppe (3.2)
eine paradoxe Zerlegung besitzt (3.3), und
zweitens in der Identifikation zweier Drehungen im
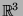 (3.6),
welche eine freie Gruppe erzeugen (3.7).
Damit kann die paradoxe Zerlegung der freien Gruppe auf typischen
(fixpunktfreien) Orbits (3.4) in kanonischer Weise zu einem
Beweis des Hausdorffschen Paradoxons herangezogen werden (3.5).
Zum Beweis des vollen PvBT sind dann nur noch vergleichsweise harmlose
Schritte nötig. Zunächst wird die abzählbare Ausnahmemenge
eliminiert (3.8), dann die erhaltene Zerlegung
der Sphäre in offensichtlicher
Weise für eine der Vollkugel ohne Mittelpunkt genutzt (3.9),
und schließlich wird noch der fehlende Mittelpunkt ergänzt (3.10).
(3.6),
welche eine freie Gruppe erzeugen (3.7).
Damit kann die paradoxe Zerlegung der freien Gruppe auf typischen
(fixpunktfreien) Orbits (3.4) in kanonischer Weise zu einem
Beweis des Hausdorffschen Paradoxons herangezogen werden (3.5).
Zum Beweis des vollen PvBT sind dann nur noch vergleichsweise harmlose
Schritte nötig. Zunächst wird die abzählbare Ausnahmemenge
eliminiert (3.8), dann die erhaltene Zerlegung
der Sphäre in offensichtlicher
Weise für eine der Vollkugel ohne Mittelpunkt genutzt (3.9),
und schließlich wird noch der fehlende Mittelpunkt ergänzt (3.10).
Das abschließende Kapitel 4 präsentiert einige Gedanken,
die sich unmittelbar ans PvBT anschließen, sowohl innermathematische
als auch außermathematische. Innermathematisch ist die wichtigste
Konsequenz des PvBT die Nichtexistenz gewisser Maße (4.1).
Somit zeigt sich, dass das PvBT kein Kuriosum darstellt, sondern
ein zentrales Resultat der Mathematik.
Daran schließen einige Überlegungen an über das Verhältnis von
Zählen (4.2) und Messen (4.3) aus mathematischer
Sicht und über das Auswahlaxiom (4.4). Dann
werden wichtige Unterschiede zwischen Mathematik und Physik anhand des
Messens erörtert (4.5) und abschließend nochmals
einige didaktische Aspekte besprochen (4.6).
2 Unendliche Mengen
2.1 Die einfachsten Paradoxien des Unendlichen
Schon früh machten Philosophen und Mathematiker bei der Analyse
des Unendlichen die Beobachtung bemerkenswerter Phänomene, welche in endlichen
Bereichen nicht auftreten können, vgl. [Ga] und [Bo].
Obwohl die Menge
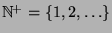 eine echte Teilmenge der Menge
eine echte Teilmenge der Menge
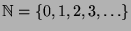 ist, liegt es nahe, beide als gleich groß anzusehen
(in Zeichen
ist, liegt es nahe, beide als gleich groß anzusehen
(in Zeichen
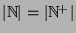 ). Schließlich
lassen sich beide Mengen in gleicher Weise als
unendliche Folgen niederschreiben, gehen also durch die
bloße Umbenennung
). Schließlich
lassen sich beide Mengen in gleicher Weise als
unendliche Folgen niederschreiben, gehen also durch die
bloße Umbenennung 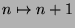 der Elemente auseinander hervor.
Im Unendlichen muss der Teil also nicht unbedingt kleiner sein als das
Ganze.
der Elemente auseinander hervor.
Im Unendlichen muss der Teil also nicht unbedingt kleiner sein als das
Ganze.
Wir geben uns damit nicht zufrieden, sondern treiben die Paradoxie
um einen Schritt weiter. So bilden die geraden Zahlen
einerseits eine echte Teilmenge
 der natürlichen
Zahlen
der natürlichen
Zahlen
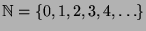 .
.
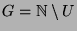 ,
,
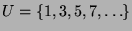 , entsteht aus
, entsteht aus 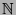 durch Weglassen
unendliche vieler Elemente, nämlich sämtlicher ungerader Zahlen
durch Weglassen
unendliche vieler Elemente, nämlich sämtlicher ungerader Zahlen 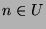 .
Andererseits füllen die Elemente von
.
Andererseits füllen die Elemente von 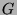 wie die von
wie die von 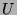 in genau derselben Weise wie die natürlichen Zahlen eine unendliche
Liste, sind also nicht wirklich weniger.
in genau derselben Weise wie die natürlichen Zahlen eine unendliche
Liste, sind also nicht wirklich weniger.
Wir können die Situation bereits im Sinn des
Titels lesen: Aus 1 wird 2 gemacht; nämlich aus einer unendlichen Menge
zwei, die gleich groß sind wie die ursprüngliche, formal
In 4.2 werden wir aber darauf zurückkommen, dass
diese Situation nicht fälschlich als Identifikation der Zahlen
1 und 2 interpretiert werden darf.
2.2 Abzählbare und überabzählbare Mengen
In moderner Sprechweise nennt man eine unendliche Menge 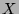 abzählbar, wenn
sich ihre Elemente mit den natürlichen Zahlen durchnummerieren lassen,
wenn man also
abzählbar, wenn
sich ihre Elemente mit den natürlichen Zahlen durchnummerieren lassen,
wenn man also
schreiben kann. Jede abzählbare Menge ist in dem Sinn gleich groß
wie 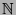 (Schreibweise:
(Schreibweise:
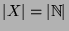 ), dass man die Elemente der beiden
Mengen einander in umkehrbar eindeutiger zuordnen kann:
), dass man die Elemente der beiden
Mengen einander in umkehrbar eindeutiger zuordnen kann: 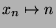 .
(Hier setzen wir voraus, dass kein Element
.
(Hier setzen wir voraus, dass kein Element 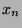 mehrmals mit verschiedenen
Indizes
mehrmals mit verschiedenen
Indizes 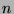 aufgelistet ist.) Ist eine unendliche Menge nicht abzählbar,
so heißt sie überabzählbar.
aufgelistet ist.) Ist eine unendliche Menge nicht abzählbar,
so heißt sie überabzählbar.
Die Menge 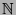 der natürlichen Zahlen ist also abzählbar
(
der natürlichen Zahlen ist also abzählbar
(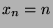 ), ebenso wie die Menge
), ebenso wie die Menge 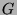 der geraden (
der geraden ( ),
),
 der ungeraden Zahlen (
der ungeraden Zahlen (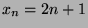 ),
),
 der Quadratzahlen (
der Quadratzahlen (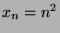 ) oder
) oder
 der Primzahlen.
der Primzahlen.
Jede unendliche Menge 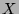 enthält eine abzählbare Teilmenge.
(Der simple Beweis macht bereits vom sogenannten Auswahlaxiom,
vgl. Abschnitt 4.4, Gebrauch:
Man wähle zuerst
enthält eine abzählbare Teilmenge.
(Der simple Beweis macht bereits vom sogenannten Auswahlaxiom,
vgl. Abschnitt 4.4, Gebrauch:
Man wähle zuerst 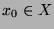 , dann
, dann 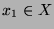 verschieden von
verschieden von 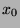 usw.,
induktiv also
usw.,
induktiv also 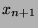 verschieden von
verschieden von
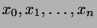 .)
Gewissermaßen sind die abzählbaren Mengen also die kleinsten unendlichen
Mengen. Es gibt aber auch abzählbare Mengen, die auf den ersten Blick größer
als
.)
Gewissermaßen sind die abzählbaren Mengen also die kleinsten unendlichen
Mengen. Es gibt aber auch abzählbare Mengen, die auf den ersten Blick größer
als 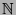 erscheinen.
erscheinen.
2.3 Abzählbarkeit von 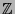
Relativ leicht sieht man, dass die Menge
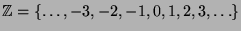 aller ganzen Zahlen abzählbar ist.
Man kann in der Aufzählung nämlich immer abwechslend positive und
negative Zahlen verwenden:
aller ganzen Zahlen abzählbar ist.
Man kann in der Aufzählung nämlich immer abwechslend positive und
negative Zahlen verwenden:
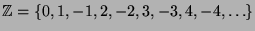 ,
also
,
also 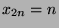 für
für 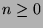 und
und 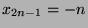 für
für 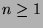 .
Grob gesprochen (d.h. 0 vernachlässigend)
hat man damit zwei Kopien der natürlichen Zahlen
(nämlich
.
Grob gesprochen (d.h. 0 vernachlässigend)
hat man damit zwei Kopien der natürlichen Zahlen
(nämlich 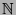 und
und 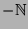 ) in einer Kopie untergebracht.
Die Analogie zur Zerlegung aus 2.1 von
) in einer Kopie untergebracht.
Die Analogie zur Zerlegung aus 2.1 von 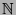 in gerade und
ungerade Zahlen liegt auf der Hand.
in gerade und
ungerade Zahlen liegt auf der Hand.
2.4 Abzählbare Vereinigungen und kartesische Produkte
Nun stellen wir uns den Ehrgeiz, nicht nur zwei Kopien,
sondern sogar (abzählbar) unendlich viele zu einer zu komprimieren.
Dazu betrachte man zum Beispiel die Menge
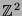 aller
ganzzahligen Gitterpunkte in der Ebene, also aller Punkte
aller
ganzzahligen Gitterpunkte in der Ebene, also aller Punkte 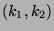 mit
mit
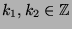 . Für jedes festgehaltene
. Für jedes festgehaltene 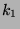 erhält man über
erhält man über
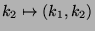 eine Kopie
eine Kopie
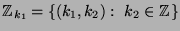 der ganzen Zahlen. Offensichtlich
ist es möglich, alle diese Gitterpunkte in einer Folge
der ganzen Zahlen. Offensichtlich
ist es möglich, alle diese Gitterpunkte in einer Folge
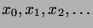 anzuordnen, indem man mit dem Punkt
anzuordnen, indem man mit dem Punkt 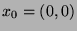 beginnt, dann (in irgendeiner Reihenfolge) alle (insgesamt acht)
Punkte nimmt, wo die betragsmäßig größte Koordinate
beginnt, dann (in irgendeiner Reihenfolge) alle (insgesamt acht)
Punkte nimmt, wo die betragsmäßig größte Koordinate
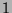 oder
oder 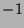 ist, also die Punkte
ist, also die Punkte
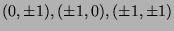 ,
dann die (insgesamt 16) Punkte mit betragsmäßig größter Komponente
,
dann die (insgesamt 16) Punkte mit betragsmäßig größter Komponente 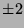 etc. Damit ist sogar allgemein
bewiesen, dass die Vereinigung (hier
etc. Damit ist sogar allgemein
bewiesen, dass die Vereinigung (hier
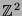 )
von abzählbar vielen abzählbaren Teilmengen (hier die
)
von abzählbar vielen abzählbaren Teilmengen (hier die
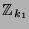 ,
,
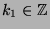 ) wieder abzählbar ist. (Ganz versteckt
und verkleidet fließt in der Aussage für Vereinigungen wieder
das Auswahlaxiom ein. Wer erkennt es?) Anders formuliert: Das kartesische Produkt
) wieder abzählbar ist. (Ganz versteckt
und verkleidet fließt in der Aussage für Vereinigungen wieder
das Auswahlaxiom ein. Wer erkennt es?) Anders formuliert: Das kartesische Produkt
von zwei abzählbaren Mengen ist wieder abzählbar. Da sich das Argument
iterieren lässt, gilt das gleiche für das kartesische Produkt
 von
von 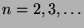 , also
beliebig endlich vielen abzählbaren Mengen
, also
beliebig endlich vielen abzählbaren Mengen 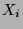 .
.
2.5 Abzählbarkeit von 
Eine interessante Folgerung ist die folgende: In der soeben konstruierten
Folge von Punkten in der Ebene interpretieren wir 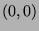 als 0,
als 0,
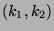 mit
mit  als rationale Zahl (Bruch)
als rationale Zahl (Bruch)
 ,
lassen davon aber nur jene stehen, welche eine Zahl darstellt, die in
der Folge nicht schon vorher aufgetreten ist. In der verbleibenden
Folge kommt also jede rationale Zahl genau einmal vor. Somit erweist
sich auch die Menge
,
lassen davon aber nur jene stehen, welche eine Zahl darstellt, die in
der Folge nicht schon vorher aufgetreten ist. In der verbleibenden
Folge kommt also jede rationale Zahl genau einmal vor. Somit erweist
sich auch die Menge  der rationalen Zahlen als abzählbar, obwohl
sie unter anderer Betrachtungsweise
scheinbar viel mehr Elemente anthält als
der rationalen Zahlen als abzählbar, obwohl
sie unter anderer Betrachtungsweise
scheinbar viel mehr Elemente anthält als  oder auch
oder auch  :
Auf der Zahlengerade liegen zwischen je zwei aufeinanderfolgenden
ganzen Zahlen unendlich viele rationale.
:
Auf der Zahlengerade liegen zwischen je zwei aufeinanderfolgenden
ganzen Zahlen unendlich viele rationale.
2.6 Abzählbarkeit der Menge endlicher Folgen
bzw. Wörter
Eine andere Variation ist die folgende: Gegeben ein Alphabet 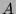 aus
endlich oder sogar abzählbar unendlich
vielen Buchstaben
aus
endlich oder sogar abzählbar unendlich
vielen Buchstaben
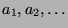 . Wir fragen
uns, wieviele Wörter (das heißt endliche Folgen) wir aus diesen Buchstaben
bilden können. (Wir wollen auch das leere Wort
. Wir fragen
uns, wieviele Wörter (das heißt endliche Folgen) wir aus diesen Buchstaben
bilden können. (Wir wollen auch das leere Wort 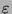 der Länge 0 zulassen.)
Nach Voraussetzung ist die Menge
der Länge 0 zulassen.)
Nach Voraussetzung ist die Menge 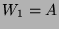 aller Wörter der Länge 1
(die also aus einem Buchstaben bestehen) endlich bzw. abzählbar.
Die Wörter der Länge 2 entsprechen in offensichtlicher Weise
den Elementen des kartesischen Produktes
aller Wörter der Länge 1
(die also aus einem Buchstaben bestehen) endlich bzw. abzählbar.
Die Wörter der Länge 2 entsprechen in offensichtlicher Weise
den Elementen des kartesischen Produktes
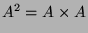 ,
bilden nach 2.4 also ebenso eine abzählbare Menge
,
bilden nach 2.4 also ebenso eine abzählbare Menge 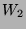 ,
wie allgemein die Menge
,
wie allgemein die Menge 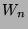 aller Wörter der Länge
aller Wörter der Länge 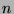 abzählbar ist.
Damit ist aber wieder nach 2.4 auch die Menge
abzählbar ist.
Damit ist aber wieder nach 2.4 auch die Menge 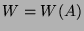 sämtlicher
endlichen Wörter als Vereinigung der abzählbar vielen
höchstens abzählbaren Mengen
sämtlicher
endlichen Wörter als Vereinigung der abzählbar vielen
höchstens abzählbaren Mengen
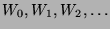 abzählbar.
(Für unendliche Wörter/Folgen siehe 2.8.)
abzählbar.
(Für unendliche Wörter/Folgen siehe 2.8.)
Wir fassen bisher besproche abzählbare Mengen bzw.
Variationen davon zusammen:
2.7 Potenzmengen sind groß
Es scheint also nicht leicht, Mengen zu konstruieren, die
nicht abzählbar sind. Die Klasse der abzählbaren Mengen
ist nach unseren bisherigen Überlegungen nämlich sehr
stabil gegenüber diversen scheinbar vergrößernden Operationen
wie der Bildung von abzählbaren Vereinigungen und
endlichen kartesischen Produkten.
Es war Cantors bahnbrechende Leistung zu erkennen, dass es
aber sehr wohl überabzählbare Mengen gibt. (Es ist keine
Übertreibung zu behaupten, dass die von Cantor begründete
Mengentheorie ihre Existenz genau dieser Tatsache verdankt.)
Und zwar bemerkte er, dass die Bildung der sogenannten
Potenzmenge 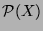 , das heißt der Menge aller Teilmengen
von
, das heißt der Menge aller Teilmengen
von 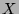 , stets zu einer größeren Menge führt. Gäbe es nämlich
eine Zuordnung
, stets zu einer größeren Menge führt. Gäbe es nämlich
eine Zuordnung
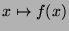 zwischen
zwischen 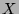 und
und 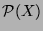 ,
in welcher als
,
in welcher als 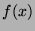 alle Teilmengen von
alle Teilmengen von 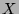 auftreten, so könnte man die Menge
auftreten, so könnte man die Menge  aller
aller  mit
mit 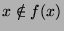 betrachten. Ist
betrachten. Ist 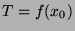 (so ein
(so ein 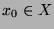 gäbe es nach Voraussetzung), so wäre
gäbe es nach Voraussetzung), so wäre
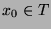 genau dann, wenn
genau dann, wenn 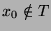 . Das ist absurd,
also kann es die gesuchte Zuordnung nicht geben.
Genau in diesem Sinne muss die Potenzmenge
. Das ist absurd,
also kann es die gesuchte Zuordnung nicht geben.
Genau in diesem Sinne muss die Potenzmenge 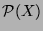 also mehr Elemente
besitzen als die ursprüngliche Menge
also mehr Elemente
besitzen als die ursprüngliche Menge 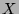 . Insbesondere ist die
Potenzmenge einer unendlichen Menge niemals abzählbar, sondern
größer, also überabzählbar.
. Insbesondere ist die
Potenzmenge einer unendlichen Menge niemals abzählbar, sondern
größer, also überabzählbar.
2.8 Überabzählbarkeit des Kontinuums
Wir wollen diesen Sachverhalt noch im Fall
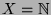 genauer unter
die Lupe nehmen.
genauer unter
die Lupe nehmen.
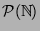 ist nach 2.7 überabzählbar.
Jeder Teilmenge
ist nach 2.7 überabzählbar.
Jeder Teilmenge 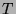 von
von 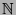 ist in natürlicher Weise
eine Folge
ist in natürlicher Weise
eine Folge
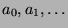 zugeordnet, indem man
zugeordnet, indem man 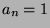 für
für 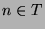 und
und 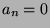 für
für 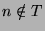 setzt. Fassen wir solche 0-1-Folgen
wiederum auf als Binärdarstellungen von reellen Zahlen
setzt. Fassen wir solche 0-1-Folgen
wiederum auf als Binärdarstellungen von reellen Zahlen
so erhalten wir eine (fast umkehrbar eindeutige) Zuordnung zwischen
Teilmengen von 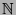 und solchen Zahlen
und solchen Zahlen 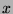 . Die
. Die 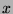 liegen alle im
Einheitsintervall
liegen alle im
Einheitsintervall ![$[0,1]$](img113.png) aller reellen Zahlen zwischen 0 und 1.
Umgekehrt besitzt jedes solche
aller reellen Zahlen zwischen 0 und 1.
Umgekehrt besitzt jedes solche 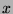 eine Binärdarstellung, die nur
dann nicht eindeutig ist, wenn ab einem gewissen Glied nur die Ziffer
0 oder nur die Ziffer 1 auftritt. Diese beiden Fälle lassen sich ineinander
überführen. (So wie sich dekadisch
eine Binärdarstellung, die nur
dann nicht eindeutig ist, wenn ab einem gewissen Glied nur die Ziffer
0 oder nur die Ziffer 1 auftritt. Diese beiden Fälle lassen sich ineinander
überführen. (So wie sich dekadisch
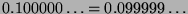 schreiben lässt.)
Diese abbrechenden unendlichen Binärdarstellungen entsprechen nämlich genau den
Zahlen
schreiben lässt.)
Diese abbrechenden unendlichen Binärdarstellungen entsprechen nämlich genau den
Zahlen
wobei
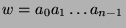 ,
,
 , irgendeine
Vorperiode bezeichnet. Dabei durchläuft
, irgendeine
Vorperiode bezeichnet. Dabei durchläuft 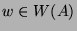 genau
sämtliche endlichen Wörter, welche nach 2.6 nur
abzählbar viele sind. Die übrigen Binärdarstellungen,
die nämlich nicht schließlich nur mehr aus Nullen oder
nur mehr aus Einsen bestehen, müssen daher überabzählbar viele sein.
(Denn abzählbar plus abzählbar ergäbe ja nur abzählbar.)
Da diese die eindeutigen Binärdarstellungen von reellen Zahlen zwischen
0 und 1 sind, ist also auch das Intervall
genau
sämtliche endlichen Wörter, welche nach 2.6 nur
abzählbar viele sind. Die übrigen Binärdarstellungen,
die nämlich nicht schließlich nur mehr aus Nullen oder
nur mehr aus Einsen bestehen, müssen daher überabzählbar viele sein.
(Denn abzählbar plus abzählbar ergäbe ja nur abzählbar.)
Da diese die eindeutigen Binärdarstellungen von reellen Zahlen zwischen
0 und 1 sind, ist also auch das Intervall ![$[0,1]$](img113.png) überabzählbar.
Durch die bijektive Zuordnung
überabzählbar.
Durch die bijektive Zuordnung
![$x \in [0,1] \mapsto a+(b-a)x \in [a,b]$](img119.png) überträgt sich diese Eigenschaft auf beliebige
nichtausgeartete Intervalle
überträgt sich diese Eigenschaft auf beliebige
nichtausgeartete Intervalle ![$[a,b]$](img120.png) .
.
Man nennt die (gemeinsame) Kardinalität = Mächtigkeit = Größe
![$\vert{\cal P}({\mathbb{N}})\vert = \vert[0,1]\vert = \vert[a,b]\vert$](img121.png) dieser Mengen übrigens auch die
Kardinalität des Kontinuums. Es sei auf einige kurze Bemerkungen zur
Kontinuumshypothese am Ende von 4.4 verwiesen.
dieser Mengen übrigens auch die
Kardinalität des Kontinuums. Es sei auf einige kurze Bemerkungen zur
Kontinuumshypothese am Ende von 4.4 verwiesen.
Wir halten fest: Das Einheitsintervall (und damit jedes
Intervall reeller Zahlen) ist überabzählbar. Desgleichen jede Menge,
in die ein Intervall eingebettet werden kann, also etwa jede eindimensionale
Kurve (zum Beispiel die Kreislinie  ) und erst recht
) und erst recht 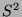 (die
zweidimensionale Oberfläche einer Kugel) oder gar
(die
zweidimensionale Oberfläche einer Kugel) oder gar 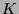 (die
dreidimensionale Vollkugel). Diese Mengen sind also alle sehr groß
im Vergleich zu abzählbaren Mengen.
(die
dreidimensionale Vollkugel). Diese Mengen sind also alle sehr groß
im Vergleich zu abzählbaren Mengen.
2.9 Große Kardinalitäten als Gegenstand der
Mengenlehre
Aus 2.7 folgt, dass von
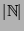 ausgehend
durch iterierte Potenzmengenbildung immer größere
Unendlichkeiten konstruiert werden können.
Die verschiedenen Unendlichkeiten steigen also selbst
unendlich an. Die Beschäftigung damit ist der Kern der Mengenlehre.
Die für uns wichtigen Mengen
ausgehend
durch iterierte Potenzmengenbildung immer größere
Unendlichkeiten konstruiert werden können.
Die verschiedenen Unendlichkeiten steigen also selbst
unendlich an. Die Beschäftigung damit ist der Kern der Mengenlehre.
Die für uns wichtigen Mengen 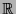 ,
,
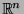 ,
, 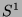 ,
, 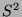 erweisen sich aber
alle als genau von der Mächtigkeit des Kontinuums.
Dass sie mindestens so groß sind,
haben wir uns bereits überlegt; dass sie nicht größer sind, brauchen wir
nicht. (Wir überlassen den Nachweis dem interessierten Leser als sehr
instruktive Übung. Bei dieser Gelegenheit wollen wir auch
auf den Satz von Schröder-Bernstein aufmerksam machen:
Ist
erweisen sich aber
alle als genau von der Mächtigkeit des Kontinuums.
Dass sie mindestens so groß sind,
haben wir uns bereits überlegt; dass sie nicht größer sind, brauchen wir
nicht. (Wir überlassen den Nachweis dem interessierten Leser als sehr
instruktive Übung. Bei dieser Gelegenheit wollen wir auch
auf den Satz von Schröder-Bernstein aufmerksam machen:
Ist 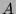 zu einer Teilmenge von
zu einer Teilmenge von 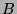 gleich mächtig und
gleich mächtig und 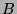 zu einer
Teilmenge von
zu einer
Teilmenge von 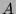 , dann sind
, dann sind 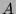 und
und 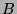 gleich mächtig.
Formal: Aus
gleich mächtig.
Formal: Aus 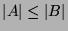 und
und 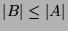 folgt
folgt 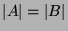 .)
.)
Nach diesem Exkurs in die Grundbegriffe unendlicher Mengen wollen
wir bisher präsentierte Ideen noch in einigen konkreten Zusammenhängen
wiederholen beziehungsweise modifizieren. Das wird sich für den
Beweis des PvBT noch als nützlich erweisen.
2.10 Hilberts Hotel
Hilbert veranschaulichte einige der behandelten Phänomene mit einem
Bild, welches als Hilberts Hotel bekannt ist.
Man stelle sich dazu ein Hotel mit abzählbar unendlich vielen
Zimmern vor, welche alle besetzt sind. Kommt nun ein weiterer
Reisender an, der Unterkunft sucht, so kann ihm leicht geholfen
werden. Sind die Zimmer
mit
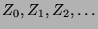 durchnummeriert, so muss lediglich
jeder Gast in das Zimmer mit der nächst höheren Nummer wechseln.
Damit wird das Zimmer
durchnummeriert, so muss lediglich
jeder Gast in das Zimmer mit der nächst höheren Nummer wechseln.
Damit wird das Zimmer  frei, und unser Neuankömmling kann einziehen.
Offenbar entspricht das genau der Beziehung
frei, und unser Neuankömmling kann einziehen.
Offenbar entspricht das genau der Beziehung
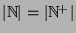 aus 2.1. (Es mag die Vorstellungskraft von Leser und Schüler anregen,
auch andere behandelte Paradoxien
des Unendlichen in den Kontext von Hilberts Hotel zu übertragen.)
aus 2.1. (Es mag die Vorstellungskraft von Leser und Schüler anregen,
auch andere behandelte Paradoxien
des Unendlichen in den Kontext von Hilberts Hotel zu übertragen.)
2.11 Hilberts Hotel auf dem Kreis aufgewickelt
Weil es auch für unsere späteren Zwecke nützlich ist, wollen wir uns
nun die Zimmer von Hilberts Hotel durch Punkte auf einer Kreislinie  dargestellt denken. Und zwar beginnen wir mit irgendeinem Punkt
dargestellt denken. Und zwar beginnen wir mit irgendeinem Punkt  .
Von diesem tragen wir einen Winkel
.
Von diesem tragen wir einen Winkel 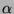 ,
,
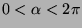 ,
(etwa im Uhrzeigersinn) auf und markieren dort
,
(etwa im Uhrzeigersinn) auf und markieren dort 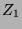 .
Wir setzen in dieser Weise fort, markieren also
.
Wir setzen in dieser Weise fort, markieren also 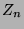 beim Winkel
beim Winkel
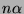 . Irgendwann werden wir erstmals eine ganze Drehung
. Irgendwann werden wir erstmals eine ganze Drehung
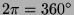 überschreiten. Wenn
überschreiten. Wenn 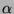 nicht gerade
von der Gestalt
nicht gerade
von der Gestalt 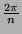 ist, werden wir aber nicht genau auf
ist, werden wir aber nicht genau auf  treffen. Ist
treffen. Ist
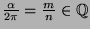 (gekürzte Darstellung)
wird uns das immerhin noch nach
(gekürzte Darstellung)
wird uns das immerhin noch nach 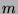 vollen Umläufen passieren.
Ist
vollen Umläufen passieren.
Ist
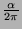 jedoch irrational (nicht als Bruch
ganzer Zahlen darstellbar), so werden wir nie einen Punkt mehrmals markieren.
Dies soll in weiterer Folge vorausgesetzt werden.
jedoch irrational (nicht als Bruch
ganzer Zahlen darstellbar), so werden wir nie einen Punkt mehrmals markieren.
Dies soll in weiterer Folge vorausgesetzt werden.
Wir haben also die Menge der Zimmer 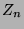 als Teilmenge von
als Teilmenge von 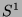 dargestellt,
man sagt auch in die Kreislinie
dargestellt,
man sagt auch in die Kreislinie 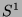 eingebettet. Dem großen Umzug
von Zimmer
eingebettet. Dem großen Umzug
von Zimmer 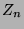 nach Zimmer
nach Zimmer 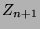 entspricht jetzt einfach
eine Drehung
entspricht jetzt einfach
eine Drehung 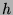 um den Winkel
um den Winkel 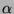 . Der Punkt
. Der Punkt  wird
dadurch frei.
wird
dadurch frei.
Bezeichne 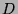 die Menge der
die Menge der 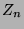 ,
,
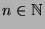 , und
, und
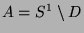 den Rest der Kreislinie. Dann gilt offenbar die Darstellung
den Rest der Kreislinie. Dann gilt offenbar die Darstellung  ,
gleichzeitig aber auch
,
gleichzeitig aber auch
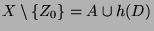 mit
jeweils disjunkten Teilmengen. Durch Anwendung der Drehung
mit
jeweils disjunkten Teilmengen. Durch Anwendung der Drehung 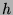 auf die Menge
auf die Menge 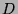 ist also ein Punkt abhandengekommen,
bzw., wenn man die Konstruktion umkehrt, dazugekommen.
Das ist das erste Beispiel einer paradoxen Zerlegung, in welcher
geometrische Objekte (Kreislinie) und größenerhaltende Bewegungen
(Drehungen) vorkommen, die dennoch Punkte gewissermaßen
herbei- oder wegzaubern.
ist also ein Punkt abhandengekommen,
bzw., wenn man die Konstruktion umkehrt, dazugekommen.
Das ist das erste Beispiel einer paradoxen Zerlegung, in welcher
geometrische Objekte (Kreislinie) und größenerhaltende Bewegungen
(Drehungen) vorkommen, die dennoch Punkte gewissermaßen
herbei- oder wegzaubern.
2.12 Absorption abzählbarer Teilmengen des Kreises
Keine großen Schwierigkeiten macht die Übertragung auf den Fall, dass man
statt mit einem Punkt  mit einer beliebigen abzählbaren Teilmenge
mit einer beliebigen abzählbaren Teilmenge 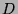 der Kreislinie
beginnt. Wir wollen eine Drehung
der Kreislinie
beginnt. Wir wollen eine Drehung 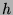 um einen geeigneten Winkel
um einen geeigneten Winkel
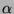 finden derart, dass iterierte Anwendung von
finden derart, dass iterierte Anwendung von 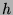 zu Mengen
zu Mengen
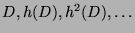 führt, die wieder paarweise disjunkt sind.
Das funktioniert im Wesentlichen deshalb, weil uns viel
mehr
führt, die wieder paarweise disjunkt sind.
Das funktioniert im Wesentlichen deshalb, weil uns viel
mehr
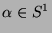 zur Auswahl stehen als Punkte
zur Auswahl stehen als Punkte 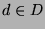 , die
Schwierigkeiten machen könnten.
, die
Schwierigkeiten machen könnten.
Etwas genauer ausgeführt lautet das Argument wie folgt:
Besteht 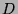 aus den Punkten
aus den Punkten
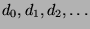 , so gibt es zu jedem Paar
, so gibt es zu jedem Paar 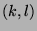 von Indizes
und jeder Potenz
von Indizes
und jeder Potenz 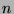 nur endlich viele Werte für
nur endlich viele Werte für 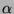 (nämlich
(nämlich
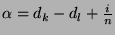 mit
mit
 ) derart,
dass
) derart,
dass
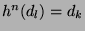 . Zu jedem Tripel
. Zu jedem Tripel
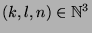 gibt
es also nur eine endliche Menge
gibt
es also nur eine endliche Menge 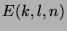 verbotener Werte für
verbotener Werte für 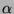 .
Wir wissen bereits, dass
.
Wir wissen bereits, dass
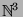 abzählbar ist. Daher ist die
gesamte Ausnahmemenge
abzählbar ist. Daher ist die
gesamte Ausnahmemenge 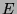 als Vereinigung der abzählbar vielen endlichen
Mengen
als Vereinigung der abzählbar vielen endlichen
Mengen 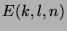 abzählbar. Es muss daher überabzählbar viele
abzählbar. Es muss daher überabzählbar viele
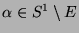 geben, von denen wir jedes wählen können.
Sei also so ein
geben, von denen wir jedes wählen können.
Sei also so ein 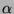 festgehalten und bezeichne
festgehalten und bezeichne 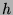 die
Drehung um den Winkel
die
Drehung um den Winkel 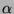 ,
, 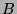 die
Vereinigung aller
die
Vereinigung aller 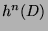 ,
,
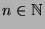 , und
, und
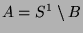 den Rest.
Dann haben wir die Darstellungen
den Rest.
Dann haben wir die Darstellungen
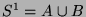 und
und
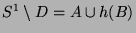 ,
wieder jeweils mit paarweise disjunkten Mengen.
Auch jede abzählbar unendliche Teilmenge
,
wieder jeweils mit paarweise disjunkten Mengen.
Auch jede abzählbar unendliche Teilmenge 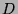 der Kreislinie kann also
her- bzw. weggedreht werden.
der Kreislinie kann also
her- bzw. weggedreht werden.
2.13 Das Gleiche nochmals mit der Sphäre
Ganz Ähnliches funktioniert, wenn wir statt der eindimensionalen
Kreislinie  die zweidimensionale Sphäre
die zweidimensionale Sphäre 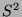 betrachten.
Sei eine beliebige höchstens abzählbare Menge
betrachten.
Sei eine beliebige höchstens abzählbare Menge 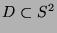 von Punkten
auf der Sphäre gegeben. Fassen wir gegenüberliegende (antipodische)
Punkte auf
von Punkten
auf der Sphäre gegeben. Fassen wir gegenüberliegende (antipodische)
Punkte auf 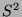 zu Paaren zusammen, so erhalten wir überabzählbar
viele Punktepaare (andernfalls wäre nach früheren Ergebnissen
zu Paaren zusammen, so erhalten wir überabzählbar
viele Punktepaare (andernfalls wäre nach früheren Ergebnissen
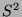 abzählbar, was nach 2.8 falsch
ist). Demnach gibt es Punktepaare, in denen
kein Partner in
abzählbar, was nach 2.8 falsch
ist). Demnach gibt es Punktepaare, in denen
kein Partner in 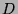 liegt. Durch ein solches Punktepaar legen wir
eine Rotationsachse
liegt. Durch ein solches Punktepaar legen wir
eine Rotationsachse 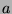 . Nach derselben Überlegung wie in 2.12
kann man einen Winkel finden, sodass für die Rotation
. Nach derselben Überlegung wie in 2.12
kann man einen Winkel finden, sodass für die Rotation 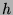 um diesen Winkel mit Achse
um diesen Winkel mit Achse 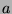 alle Mengen
alle Mengen
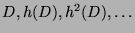 paarweise disjunkt sind. Wie für
paarweise disjunkt sind. Wie für 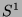 induziert das auch Zerlegungen
induziert das auch Zerlegungen
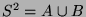 und
und
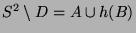 .
.
2.14 Das Konzept der Zerlegungsäquivalenz
In solchen Situationen wie den in den drei
letzten Abschnitten behandelten sprechen wir von
zerlegungsgleichen Mengen und schreiben
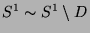 bzw.
bzw.
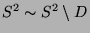 .
.
Vermutlich wird der Leser das Paradoxe an den bisher behandelten Beispielen
bei weitem nicht so beeindruckend finden wie im PvBT. Das liegt
wohl daran, dass die Menge 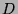 , die her- oder
weggezaubert werden kann, sehr klein (abzählbar) ist im Vergleich zu den
überabzählbaren Mengen
, die her- oder
weggezaubert werden kann, sehr klein (abzählbar) ist im Vergleich zu den
überabzählbaren Mengen 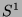 und
und 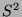 . Tatsächlich lässt sich in
maßtheoretischer Hinsicht damit auch nichts Außergewöhnliches gewinnen.
Die Menge
. Tatsächlich lässt sich in
maßtheoretischer Hinsicht damit auch nichts Außergewöhnliches gewinnen.
Die Menge 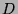 hat einfach das Maß 0.
hat einfach das Maß 0.
Dennoch werden wir die gewonnen Einsichten noch erfolgreich einsetzen
können. Als wesentlichen Schritt in Richtung PvBT werden wir
nämlich das Hausdorffsche
Paradoxon beweisen, welches eine paradoxe Zerlegung von
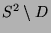 liefert, wobei
liefert, wobei 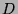 abzählbar ist. Die Zerlegungsäquivalenz zu
abzählbar ist. Die Zerlegungsäquivalenz zu 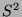 wird dann zu einer paradoxen Zerlegung von ganz
wird dann zu einer paradoxen Zerlegung von ganz 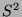 führen.
führen.
3 Der Beweis des Paradoxons von Banach-Tarski
3.1 Hausdorffs wichtiger Beitrag
Wie bereits angekündigt, werden wir zunächst eine paradoxe
Zerlegung von
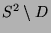 konstruieren, wobei
konstruieren, wobei 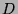 eine geeignete
abzählbare Menge ist. Genauer: Wir werden
eine geeignete
abzählbare Menge ist. Genauer: Wir werden
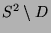 in paarweise
disjunkte Mengen
in paarweise
disjunkte Mengen
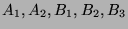 zerlegen und zu diesen
zwei Drehungen
zerlegen und zu diesen
zwei Drehungen  und
und  finden derart, dass
finden derart, dass
gilt.
Als  werden wir eine Drehung um einen geeigneten
Winkel
werden wir eine Drehung um einen geeigneten
Winkel 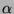 mit der
mit der 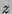 -Achse als Rotationsachse wählen.
Ist
-Achse als Rotationsachse wählen.
Ist 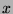 ein beliebiger Punkt auf der Sphäre, wobei wir nur
die beiden Fixpunkte, nämlich Nord- und
Südpol ausschließen, so zeigen die Überlegungen aus 2.11,
dass die Punkte
ein beliebiger Punkt auf der Sphäre, wobei wir nur
die beiden Fixpunkte, nämlich Nord- und
Südpol ausschließen, so zeigen die Überlegungen aus 2.11,
dass die Punkte
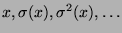 (der sogenannte
(der sogenannte
 -Orbit von
-Orbit von 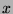 ) alle verschieden sind.
Entsprechendes gilt, wenn wir z.B. statt der
) alle verschieden sind.
Entsprechendes gilt, wenn wir z.B. statt der 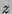 -Achse die
-Achse die 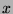 -Achse
als Rotationsachse wählen und die beiden Punkte verbieten, in welchen
sie
-Achse
als Rotationsachse wählen und die beiden Punkte verbieten, in welchen
sie 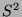 schneidet. Wir kommen darauf später zurück.
schneidet. Wir kommen darauf später zurück.
Es soll darauf hingewiesen werden, dass der
maßtheoretische Kern des PvBT (für die zweidimensionale
Kugeloberfläche statt für die dreidimensionale Vollkugel)
bereits mit dem Abschluss des Beweises des Hausdorffschen Paradoxons in
3.7 bewältigt sein wird. Gibt man nämlich der
überabzählbaren Menge 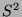 das Maß 1, so wird man der abzählbaren
Teilmenge
das Maß 1, so wird man der abzählbaren
Teilmenge 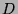 sinnvollerweise nur das Maß 0 zuordnen können.
Denn jedes endliche Vielfache einer abzählbaren Menge ist wieder
abzählbar. Endliche Vielfache von
sinnvollerweise nur das Maß 0 zuordnen können.
Denn jedes endliche Vielfache einer abzählbaren Menge ist wieder
abzählbar. Endliche Vielfache von 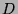 können also niemals
ganz
können also niemals
ganz 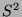 ausmachen. Wäre das Maß von
ausmachen. Wäre das Maß von 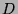 positiv, so wäre demnach
jenes von
positiv, so wäre demnach
jenes von 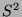 größer als jedes endliche Vielfache dieser Zahl,
somit unendlich.
größer als jedes endliche Vielfache dieser Zahl,
somit unendlich.
Was in der paradoxen Zerlegung auf ganz 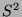 noch fehlt, ist für den Maßtheoretiker also vernachlässigbar.
Insofern scheint es berechtigt, den Beweis des Hausdorffschen
Paradoxons als den Kern im Beweis des PvBT zu betrachten.
noch fehlt, ist für den Maßtheoretiker also vernachlässigbar.
Insofern scheint es berechtigt, den Beweis des Hausdorffschen
Paradoxons als den Kern im Beweis des PvBT zu betrachten.
3.2 Die von zwei Elementen frei erzeugte Gruppe
Wir fragen uns, was wir erhalten, wenn wir
zunächst nicht näher bestimmte Drehungen  und
und
 in beliebiger Reihenfolge und in positiver und negativer
Richtung auf
in beliebiger Reihenfolge und in positiver und negativer
Richtung auf 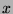 anwenden. Als
sogenannte Orbitpunkte erhalten wir also beispielsweise
anwenden. Als
sogenannte Orbitpunkte erhalten wir also beispielsweise
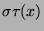 ,
,
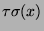 ,
,
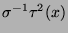 etc.
Man beachte, dass es keinen Grund gibt anzunehmen, dass manche dieser
Punkte übereinstimmen. Insbesondere gilt allgemein kein Kommutativgesetz.
etc.
Man beachte, dass es keinen Grund gibt anzunehmen, dass manche dieser
Punkte übereinstimmen. Insbesondere gilt allgemein kein Kommutativgesetz.
Wollen wir die Situation formal fassen, bietet es sich an, die
Sprechweise aus 2.6 zu wählen. Wir haben also
(endliche) Wörter 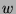 mit Buchstaben oder Symbolen
mit Buchstaben oder Symbolen
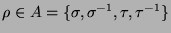 zu bilden.
Wir dürfen außerdem verlangen, dass
zu bilden.
Wir dürfen außerdem verlangen, dass 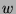 reduziert ist, das heißt,
dass die beiden Symbole
reduziert ist, das heißt,
dass die beiden Symbole  und
und
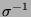 nicht unmittelbar hintereinander stehen, da man sie ja
sonst wegkürzen könnte. Die Menge all dieser Wörter trägt eine
Gruppenstruktur: Als Produkt zweier Wörter
nicht unmittelbar hintereinander stehen, da man sie ja
sonst wegkürzen könnte. Die Menge all dieser Wörter trägt eine
Gruppenstruktur: Als Produkt zweier Wörter 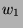 und
und 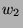 haben wir einfach
das Kompositum
haben wir einfach
das Kompositum 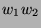 zu nehmen. Stoßen an der Schnittstelle zwei
Symbole
zu nehmen. Stoßen an der Schnittstelle zwei
Symbole 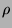 und
und 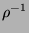 zusammen, dann können wir durch Wegkürzen
erzwingen, dass auch das Produkt ein reduziertes Wort ist.
zusammen, dann können wir durch Wegkürzen
erzwingen, dass auch das Produkt ein reduziertes Wort ist.
Beispiel: Für
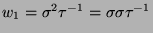 und
und
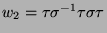 kürzen sich in
kürzen sich in 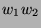 die letzten beiden Glieder von
die letzten beiden Glieder von 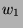 gegen die ersten beiden von
gegen die ersten beiden von
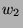 weg, und wir erhalten
weg, und wir erhalten
Zum Nachweis der Gruppeneigenschaften ist nur zu bemerken, dass
man in der beschriebenen Weise wirklich wieder reduzierte Worte erhält,
dass offenbar das Assoziativgesetz
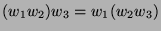 gilt,
dass das leere Wort
gilt,
dass das leere Wort
 die Rolle des neutralen Elements spielt
und dass jedes Wort
die Rolle des neutralen Elements spielt
und dass jedes Wort
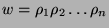 ein Inverses,
nämlich
ein Inverses,
nämlich
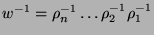 besitzt.
(Hier ist natürlich
besitzt.
(Hier ist natürlich
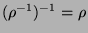 für
für
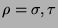 zu vereinbaren.)
zu vereinbaren.)
Die Menge 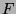 aller reduzierten Wörter mit der beschriebenen
Gruppenstruktur heißt auch die von den Symbolen
aller reduzierten Wörter mit der beschriebenen
Gruppenstruktur heißt auch die von den Symbolen  und
und  frei erzeugte Gruppe. Wenn wir kurz von der freien Gruppe sprechen,
werden wir immer diese Gruppe meinen.
frei erzeugte Gruppe. Wenn wir kurz von der freien Gruppe sprechen,
werden wir immer diese Gruppe meinen.
Wegen
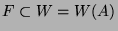 ,
,
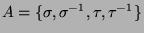 ,
ist
,
ist 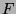 nach 2.6 abzählbar. Von dieser Tatsache
werden wir wiederholt Gebrauch machen.
nach 2.6 abzählbar. Von dieser Tatsache
werden wir wiederholt Gebrauch machen.
Eine kurze und etwas ungenaue Bemerkung zum Wort frei:
Wir können hier nicht auf die sehr
interessanten und allgemeinen Eigenschaften freier Gruppen (oder noch
allgemeiner: freier Objekte) eingehen. In unserem Kontext genügt es,
wenn man sich vorstellt, dass die freie Gruppe frei ist von
(einschränkenden) Gesetzen, die
nicht allein aus den Gruppenaxiomen folgen. So folgt beispielsweise das
Kommutativgesetz nicht allgemein und gilt tatsächlich nicht in 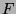 .
.
3.3 Hausdorffs entscheidende Beobachtung:
Eine paradoxe Zerlegung der freien Gruppe
Eine wichtige Vorstellung, die der Mathematiker mit dem Begriff
der Gruppe verbindet, besteht darin,
dass jedes Gruppenelement 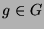 als Transformation
als Transformation
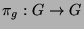 ,
,
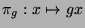 , der Gruppe auf sich selbst
interpretiert werden kann.
(Dieses Faktum ist auch als Darstellungssatz von Cayley bekannt,
wobei es vor allem um die Relation
, der Gruppe auf sich selbst
interpretiert werden kann.
(Dieses Faktum ist auch als Darstellungssatz von Cayley bekannt,
wobei es vor allem um die Relation
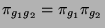 geht.)
Diese Transformationen sind stets umkehrbar eindeutig, bewahren also
gewissermaßen alle Informationen. Bei kommutativen Gruppen wie
geht.)
Diese Transformationen sind stets umkehrbar eindeutig, bewahren also
gewissermaßen alle Informationen. Bei kommutativen Gruppen wie 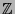 oder
oder
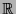 sind die
sind die 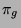 Translationen (Verschiebungen) um die additive
Konstante
Translationen (Verschiebungen) um die additive
Konstante 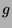 . Das entspricht der in diesem Fall unverfänglichen Intuition,
dass die durch Gruppenelemente induzierten Transformationen die
Größe von Mengen nicht verändern.
. Das entspricht der in diesem Fall unverfänglichen Intuition,
dass die durch Gruppenelemente induzierten Transformationen die
Größe von Mengen nicht verändern.
Der erste entscheidende Schritt für den
Beweis des RvBT ist die einfache Beobachtung, dass im Fall der
freien Gruppe etwas passiert, was dieser Intuition widerspricht.
Es liegt nämlich nahe, die Wörter in 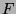 einzuteilen nach Anfangssymbol.
Bezeichne also
einzuteilen nach Anfangssymbol.
Bezeichne also 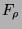 die Menge jener
die Menge jener 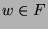 , welche mit dem Symbol
, welche mit dem Symbol
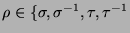 beginnen,
so liegt die Partition
beginnen,
so liegt die Partition
auf der Hand. Vernachlässigen wir die Einermenge
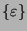 , so stellt
jedes
, so stellt
jedes 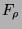 gewissermaßen ein Viertel von
gewissermaßen ein Viertel von 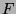 dar.
Multiplizieren wir aber Elemente
dar.
Multiplizieren wir aber Elemente
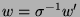 aus
aus
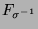 von links mit
von links mit  , so kürzt sich das erste
Symbol weg, und es bleibt
, so kürzt sich das erste
Symbol weg, und es bleibt 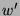 übrig. Die einzige Einschränkung für
übrig. Die einzige Einschränkung für 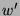 ergibt sich aus der Reduziertheit von
ergibt sich aus der Reduziertheit von 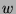 . Das bedeutet, dass
. Das bedeutet, dass 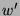 nicht
mit
nicht
mit  beginnen kann. Da alles andere möglich ist, kann
beginnen kann. Da alles andere möglich ist, kann 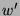 ein beliebiges Element in
ein beliebiges Element in
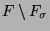 sein.
In obiger Schreibweise notiert bedeutet das
sein.
In obiger Schreibweise notiert bedeutet das
Aus dem Viertel
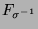 wurde durch Anwendung der Transformation
wurde durch Anwendung der Transformation
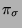 also ein Dreiviertel von
also ein Dreiviertel von 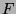 .
Da sich das gleiche Spiel mit
.
Da sich das gleiche Spiel mit  statt
statt  treiben lässt,
kann man ebenso das Viertel
treiben lässt,
kann man ebenso das Viertel 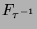 zum Dreiviertel
zum Dreiviertel
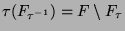 aufblasen.
In Mengengleichungen haben wir also, wenn wir
aufblasen.
In Mengengleichungen haben wir also, wenn wir
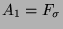 ,
,
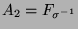 ,
,
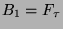 ,
,
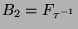 und
und
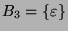 setzen und für
setzen und für 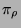 kurz
kurz 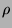 schreiben,
die an 3.1 erinnernde paradoxe Zerlegung
schreiben,
die an 3.1 erinnernde paradoxe Zerlegung
Wir werden diese Zerlegung von Mengen formaler Zeichenketten
verwenden, um auch zu geometrisch
paradox anmutenden Zerlegungen wie im PvBT zu gelangen.
3.4 Typische Orbits unter der freien Gruppe
In der Definition der freien Gruppe mit den Erzeugenden  und
und  wurde überhaupt nicht von einer Interpretation dieser beiden Elemente
als Rotationen oder auch nur als Abbildungen Gebrauch gemacht.
Die freie Gruppe ist in diesem Sinne ein rein formales, nur Symbole
und deren Manipulation voraussetzendes Objekt.
wurde überhaupt nicht von einer Interpretation dieser beiden Elemente
als Rotationen oder auch nur als Abbildungen Gebrauch gemacht.
Die freie Gruppe ist in diesem Sinne ein rein formales, nur Symbole
und deren Manipulation voraussetzendes Objekt.
Die für uns entscheidende Frage ist, ob sich die Orbits
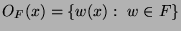 eines Punktes
eines Punktes 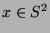 unter
unter 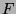 so verhalten können wie die freie Gruppe
so verhalten können wie die freie Gruppe 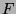 selbst.
Dabei fassen wir die Worte
selbst.
Dabei fassen wir die Worte 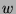 jetzt als Rotationen
im
jetzt als Rotationen
im
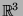 auf, welche sich aus den erzeugenden Rotationen
auf, welche sich aus den erzeugenden Rotationen  und
und  und deren Inversen zusammensetzen. Wunschgemäßes Verhalten tritt
offenbar genau dann auf,
wenn
und deren Inversen zusammensetzen. Wunschgemäßes Verhalten tritt
offenbar genau dann auf,
wenn 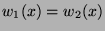 nur bei Übereinstimmung der reduzierten Wörter
nur bei Übereinstimmung der reduzierten Wörter 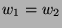 als solcher vorliegt. Da die Gleichung
als solcher vorliegt. Da die Gleichung 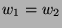 mit
mit
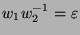 äquivalent ist, kann man die Bedingung auch so ausdrücken:
äquivalent ist, kann man die Bedingung auch so ausdrücken:
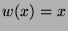 nur für
nur für
 . Wir sagen in diesem Fall, dass
. Wir sagen in diesem Fall, dass 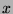 kein
Fixpunkt von
kein
Fixpunkt von 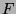 ist und wollen den Orbit
ist und wollen den Orbit 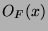 fixpunktfrei oder typisch nennen.
fixpunktfrei oder typisch nennen.
Für einen typischen Orbit 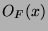 können wir die paradoxe Zerlegung von
können wir die paradoxe Zerlegung von 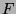 aus 3.3
offenbar unmittelbar übertragen zur entsprechenden paradoxen Zerlegung
aus 3.3
offenbar unmittelbar übertragen zur entsprechenden paradoxen Zerlegung
von 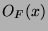 .
.
3.5 Das Zusammensetzen der typischen Orbits
Die paradoxe Zerlegung eines typischen Orbits lässt sich in (fast)
trivialer Weise auf die Vereinigung 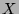 aller typischen Orbits übertragen.
aller typischen Orbits übertragen.
Zunächst ist klar, dass
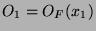 und
und
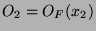 entweder
disjunkt oder identisch sind.
(Sei
entweder
disjunkt oder identisch sind.
(Sei
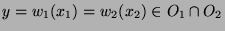 , dann folgt aus
, dann folgt aus
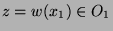 auch
auch
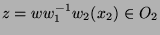 , also
, also
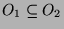 . Analog gilt
. Analog gilt
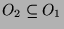 , also
, also 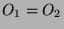 .)
.)
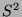 ist also die disjunkte Zerlegung sämtlicher Orbits.
Aus jedem typischen Orbit
ist also die disjunkte Zerlegung sämtlicher Orbits.
Aus jedem typischen Orbit 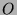 sei nun ein
sei nun ein 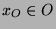 ausgewählt.
Als
ausgewählt.
Als 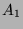 wählen wir die Vereinigung aller
wählen wir die Vereinigung aller 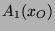 ,
wobei
,
wobei 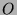 sämtliche typischen Orbits durchläuft. In völlig analoger
Weise definiert man
sämtliche typischen Orbits durchläuft. In völlig analoger
Weise definiert man 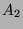 ,
,  ,
,  und
und  und erhält eine
paradoxe Zerlegung der Vereinigung
und erhält eine
paradoxe Zerlegung der Vereinigung 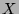 aller typischen Orbits.
aller typischen Orbits.
(Dass es zu jeder disjunkten Menge nichtleerer Mengen so eine
Auswahlfunktion 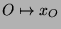 gibt, ist genau die Aussage des
sogenannten Auswahlaxioms aus der Mengenlehre.
Manche Mathematiker legen Wert darauf, penibel anzugeben,
wenn sie dieses Axiom verwendet haben. Einzelne Vereinsamte lehnen seine
Verwendung sogar generell ab. Doch mehr davon in 4.4.)
gibt, ist genau die Aussage des
sogenannten Auswahlaxioms aus der Mengenlehre.
Manche Mathematiker legen Wert darauf, penibel anzugeben,
wenn sie dieses Axiom verwendet haben. Einzelne Vereinsamte lehnen seine
Verwendung sogar generell ab. Doch mehr davon in 4.4.)
Wir sind mit dem Beweis des Hausdorffschen Paradoxons fertig,
wenn wir zeigen können, dass die Restmenge
bei geeigneter Wahl von
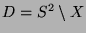 abzählbar ist.
Hierzu eine geometrische Überlegung.
abzählbar ist.
Hierzu eine geometrische Überlegung.
Jedes 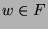 repräsentiert eine Bewegungung, welche als Komposition
von
repräsentiert eine Bewegungung, welche als Komposition
von  und
und  und ihren Inversen zustandekommt.
Angenommen, es handelt sich dabei nicht um die identische Abbildung
und ihren Inversen zustandekommt.
Angenommen, es handelt sich dabei nicht um die identische Abbildung 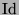 ,
welche alle Punkte fest lässt. Sei dennoch
,
welche alle Punkte fest lässt. Sei dennoch 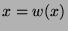 ein
Fixpunkt von
ein
Fixpunkt von 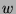 . (Die aus der Linearen Algebra bekannte
Tatsache, dass jedes derartige
. (Die aus der Linearen Algebra bekannte
Tatsache, dass jedes derartige 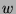 in
in
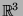 wirklich zwei Fixpunkte hat,
benötigen wir hier nicht einmal.) Dann handelt es sich bei
wirklich zwei Fixpunkte hat,
benötigen wir hier nicht einmal.) Dann handelt es sich bei 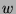 offenbar um eine Drehung um eine Rotationsachse, die
durch
offenbar um eine Drehung um eine Rotationsachse, die
durch 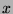 und den gegenüberliegenden (antipodischen) Punkt
und den gegenüberliegenden (antipodischen) Punkt 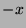 geht.
Alle übrigen Punkte werden durch
geht.
Alle übrigen Punkte werden durch 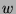 bewegt und bleiben nicht fix.
Jedes
bewegt und bleiben nicht fix.
Jedes
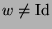 hat also nur zwei Fixpunkte.
hat also nur zwei Fixpunkte.
Angenommen, nur das leere Wort 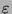 stellt die identische Abbildung dar,
so liefern die abzählbar vielen
stellt die identische Abbildung dar,
so liefern die abzählbar vielen
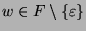 also nur abzählbar viele Fixpunkte
also nur abzählbar viele Fixpunkte 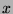 .
Jedes solche
.
Jedes solche 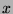 hat einen höchstens abzählbaren Orbit
hat einen höchstens abzählbaren Orbit 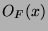 ,
somit machen die nicht typischen Orbits nur eine abzählbare Ausnahmemenge
,
somit machen die nicht typischen Orbits nur eine abzählbare Ausnahmemenge
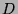 aus, und der Beweis ist fertig.
aus, und der Beweis ist fertig.
Offen bleibt also lediglich die Frage,
ob  und
und  geeignet gewählt werden
können derart, dass tatsächlich nur das leere Wort die identische
Abbildung darstellt. Es erscheint sehr plausibel, dass dies möglich ist.
Schließlich müssen nur die abzählbar vielen Bedingungen
geeignet gewählt werden
können derart, dass tatsächlich nur das leere Wort die identische
Abbildung darstellt. Es erscheint sehr plausibel, dass dies möglich ist.
Schließlich müssen nur die abzählbar vielen Bedingungen
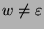 ,
,
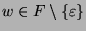 , erfüllt werden,
während für die Rotationswinkel und die Winkel der beiden Rotationsachsen
zueinander überabzählbar viele Werte zur Verfügung stehen.
Wie die nachfolgenden Argumente zeigen, führt uns diese
Plausibilitätsüberlegung nicht in die Irre.
, erfüllt werden,
während für die Rotationswinkel und die Winkel der beiden Rotationsachsen
zueinander überabzählbar viele Werte zur Verfügung stehen.
Wie die nachfolgenden Argumente zeigen, führt uns diese
Plausibilitätsüberlegung nicht in die Irre.
3.6 Die Abbildungsgleichungen geeigneter Rotationen
Wir wollen uns aber mit dem Plausibilitätsargument aus 3.5
nicht zufriedengeben. Glücklicherweise lassen sich sehr einfach
zwei konkrete Wahlen von  und
und  angeben, die
freie Erzeugende einer freien Untergruppe der vollen Drehgruppe sind.
Und zwar kann man zwei Rotationen mit orthogonalen Achsen
und dem Rotationswinkel
angeben, die
freie Erzeugende einer freien Untergruppe der vollen Drehgruppe sind.
Und zwar kann man zwei Rotationen mit orthogonalen Achsen
und dem Rotationswinkel
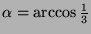 wählen.
wählen.
Sei
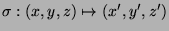 durch folgende
Gleichungen definiert.
durch folgende
Gleichungen definiert.
Die Abbildung  verändert nichts an der
verändert nichts an der 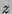 -Koordinate,
während umgekehrt
-Koordinate,
während umgekehrt 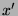 und
und 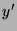 nur von
nur von 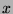 und
und 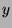 , nicht aber
von
, nicht aber
von 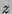 abhängen. Die Transformation
abhängen. Die Transformation  wird deshalb hinreichend verstanden, wenn klar ist, was sie für
wird deshalb hinreichend verstanden, wenn klar ist, was sie für  ,
also innerhalb der
,
also innerhalb der 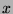 -
-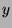 -Ebene bewirkt. Innerhalb dieser wird der
Punkt
-Ebene bewirkt. Innerhalb dieser wird der
Punkt 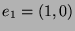 auf den Punkt
auf den Punkt
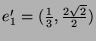 abgebildet. Da
abgebildet. Da 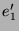 nach dem pythagoräischen Lehrsatz ebenso wie
nach dem pythagoräischen Lehrsatz ebenso wie
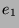 auf dem Einheitskreis liegt, entspricht das zunächst für
diesen Punkt tatsächlich einer Drehung mit Drehzentrum im Ursprung.
Der Drehwinkel
auf dem Einheitskreis liegt, entspricht das zunächst für
diesen Punkt tatsächlich einer Drehung mit Drehzentrum im Ursprung.
Der Drehwinkel 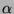 ist durch die Gleichungen
ist durch die Gleichungen
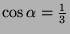 ,
,
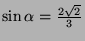 bestimmt,
also
bestimmt,
also
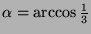 . Die analoge Überlegung für
. Die analoge Überlegung für 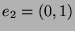 und
und
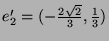 bestätigt das auch für den
anderen Basispunkt.
bestätigt das auch für den
anderen Basispunkt.  bewahrt als lineare Abbildung
Linearkombinationen; jeder beliebige
Punkt der Grundebenebene
bewahrt als lineare Abbildung
Linearkombinationen; jeder beliebige
Punkt der Grundebenebene  ist Linearkombination der beiden
Basisvektoren
ist Linearkombination der beiden
Basisvektoren 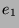 und
und 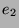 . Deshalb dreht
. Deshalb dreht  jeden Punkt dieser
Ebene um den Ursprung
jeden Punkt dieser
Ebene um den Ursprung  und jede dazu parallele Ebene
und jede dazu parallele Ebene 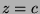 ,
,
 ,
um den Punkt
,
um den Punkt 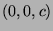 , jeweils um denselben Winkel
, jeweils um denselben Winkel 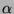 .
Also stellen obige
Abbildungsgleichungen für
.
Also stellen obige
Abbildungsgleichungen für  die Drehung um den Winkel
die Drehung um den Winkel
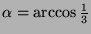 mit der
mit der 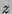 -Achse als Rotationsachse dar.
(Diese vielleicht etwas umständlich anmutende geometrische Überlegung
wurde so dargestellt, um eine Möglichkeit zur Vermeidung
des in der Schule nicht zum Standardrepertoir gehörenden
Matrizenkalküls zu skizzieren.)
-Achse als Rotationsachse dar.
(Diese vielleicht etwas umständlich anmutende geometrische Überlegung
wurde so dargestellt, um eine Möglichkeit zur Vermeidung
des in der Schule nicht zum Standardrepertoir gehörenden
Matrizenkalküls zu skizzieren.)
Ganz analog überlegt man sich, dass die Drehung
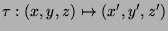 um die
um die
 -Achse um denselben Winkel
-Achse um denselben Winkel
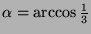 durch die Gleichungen
durch die Gleichungen
beschrieben wird.
Außerdem sei darauf hingewiesen, dass bei der Umkehrung der
Rotationsrichtung, d.h. bei Ersetzung von  und
und  durch
durch 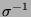 bzw.
bzw. 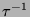 in den Abbildungsgleichungen
nur die Vorzeichen der Ausdrücke vom Betrag
in den Abbildungsgleichungen
nur die Vorzeichen der Ausdrücke vom Betrag
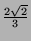 geändert werden müssen.
geändert werden müssen.
3.7 Eine kurze Rechnung
Um zu beweisen, dass die angegebenen Drehungen  und
und  wirklich eine freie Gruppe erzeugen, müssen wir zeigen, dass
jedes reduzierte Wort
wirklich eine freie Gruppe erzeugen, müssen wir zeigen, dass
jedes reduzierte Wort
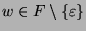 eine
Rotation verschieden von der Identität darstellt. Dafür genügt es,
einen einzigen Punkt zu finden, der nicht auf sich abgebildet wird.
Hört
eine
Rotation verschieden von der Identität darstellt. Dafür genügt es,
einen einzigen Punkt zu finden, der nicht auf sich abgebildet wird.
Hört 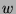 mit einer positiven oder negativen Potenz von
mit einer positiven oder negativen Potenz von  auf, so erweist sich der Punkt
auf, so erweist sich der Punkt  als geeignet; im anderen
Fall, dass nämlich
als geeignet; im anderen
Fall, dass nämlich 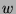 mit einer positiven oder negativen Potenz
von
mit einer positiven oder negativen Potenz
von  aufhört, muss dann aus Symmetriegründen der Punkt
aufhört, muss dann aus Symmetriegründen der Punkt  die entsprechende Eigenschaft haben. Wir dürfen uns für den Beweis
daher auf den ersten Fall beschränken.
die entsprechende Eigenschaft haben. Wir dürfen uns für den Beweis
daher auf den ersten Fall beschränken.
Durch vollständige Induktion nach der Länge 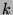 von
von 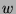 überzeugt man
sich davon, dass
überzeugt man
sich davon, dass
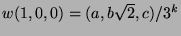 gilt mit ganzen
Zahlen
gilt mit ganzen
Zahlen 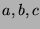 . Für
. Für 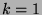 ist das unmittelbar durch Einsetzen
in die Abbildungsgleichungen aus 3.6 ersichtlich.
Für
ist das unmittelbar durch Einsetzen
in die Abbildungsgleichungen aus 3.6 ersichtlich.
Für 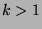 hat man die vier möglichen Fälle für
das erste Symbol
hat man die vier möglichen Fälle für
das erste Symbol 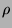 in
in 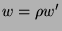 zu unterscheiden.
Mit
zu unterscheiden.
Mit
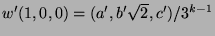 (Induktionsannahme) erhält man
durch Einsetzen in die Abbildungsgleichung von
(Induktionsannahme) erhält man
durch Einsetzen in die Abbildungsgleichung von 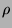 im Fall
im Fall
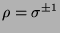 die Rekursion
die Rekursion
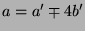 ,
,
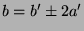 ,
, 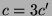 ; im Fall
; im Fall
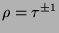 entsprechend
entsprechend 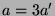 ,
,
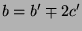 ,
,
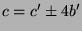 . Das zeigt die Ganzzahligkeit von
. Das zeigt die Ganzzahligkeit von  .
.
Offen ist nur noch
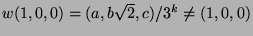 .
Dazu genügt der Nachweis, dass
.
Dazu genügt der Nachweis, dass  nicht durch 3 teilbar ist.
Besteht
nicht durch 3 teilbar ist.
Besteht  nur aus einem Symbol, welches
dann in unserem Fall
nur aus einem Symbol, welches
dann in unserem Fall
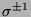 sein muss, so ist
sein muss, so ist 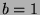 tatsächlich nicht durch 3 teilbar.
Ist das Wort
tatsächlich nicht durch 3 teilbar.
Ist das Wort 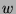 länger, so sind
für die ersten zwei Symbole
länger, so sind
für die ersten zwei Symbole
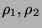 in
in
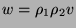 vier Möglichkeiten zu unterscheiden, nämlich
vier Möglichkeiten zu unterscheiden, nämlich
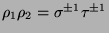 ,
,
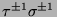 ,
,
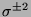 oder
oder 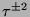 .
Im ersten Fall erhält man aus der Rekursion ein durch 3 teilbares
.
Im ersten Fall erhält man aus der Rekursion ein durch 3 teilbares
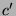 , also kann mit
, also kann mit 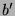 auch
auch
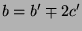 nicht durch 3 teilbar
sein. Ähnlich verhält sich der zweite Fall mit
nicht durch 3 teilbar
sein. Ähnlich verhält sich der zweite Fall mit
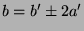 und durch
3 teilbarem
und durch
3 teilbarem 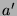 . In den verbleibenden beiden Fällen muss man
in der Rekursion einen Schritt weiter zurückgreifen und
. In den verbleibenden beiden Fällen muss man
in der Rekursion einen Schritt weiter zurückgreifen und
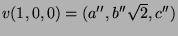 heranziehen. In beiden Fällen
erhält man (hier für den dritten Fall durchgeführt) mit Hilfe der Rekursion
heranziehen. In beiden Fällen
erhält man (hier für den dritten Fall durchgeführt) mit Hilfe der Rekursion
Die Eigenschaft, nicht durch 3 teilbar zu sein, vererbt sich also
von 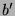 auf
auf 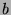 .
.
Damit ist der Beweis des Hausdorffschen Paradoxons, wie es in 3.1
formuliert wurde, erbracht.
3.8 Eine paradoxe Zerlegung der Sphäre
Der Schritt zu einer paradoxen Zerlegung der gesamten Kugeloberfläche
liegt auf der Hand. Wir wissen nämlich einerseits aus den letzten
Abschnitten, dass es eine abzählbare Teilmenge 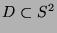 gibt,
so dass
gibt,
so dass
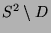 eine paradoxe Zerlegung besitzt.
Andererseits wissen wir aus 2.13 und 2.14,
dass
eine paradoxe Zerlegung besitzt.
Andererseits wissen wir aus 2.13 und 2.14,
dass
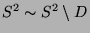 zerlegungsäquivalent
sind. Wir müssen uns also nur überlegen, dass sich die Existenz
paradoxer Zerlegungen auf zerlegungsäquivalente Objekte überträgt.
Dies zeigt die folgende Überlegung, in der wir bewusst auf
formalere Notationen verzichten.
zerlegungsäquivalent
sind. Wir müssen uns also nur überlegen, dass sich die Existenz
paradoxer Zerlegungen auf zerlegungsäquivalente Objekte überträgt.
Dies zeigt die folgende Überlegung, in der wir bewusst auf
formalere Notationen verzichten.
Seien also  zerlegungsäquivalent. Der
Zerlegungsäquivalenz entsprechen Zerlegungen von
zerlegungsäquivalent. Der
Zerlegungsäquivalenz entsprechen Zerlegungen von 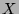 und
und 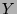 in
gleich viele Teile
in
gleich viele Teile 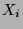 bzw.
bzw. 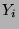 , von denen entsprechende durch
Bewegungen
, von denen entsprechende durch
Bewegungen  (in unserem Fall durch Drehungen) ineinander übergeführt
werden können. Gleichzeitig besitze
(in unserem Fall durch Drehungen) ineinander übergeführt
werden können. Gleichzeitig besitze 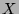 eine paradoxe Zerlegung
in Mengen
eine paradoxe Zerlegung
in Mengen 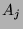 und
und 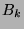 , wo die Bewegungen
, wo die Bewegungen 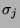 und
und 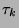 auftreten. Will man eine paradoxe Zerlegung von
auftreten. Will man eine paradoxe Zerlegung von 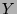 konstruieren,
baut man seine Bruchstücke
konstruieren,
baut man seine Bruchstücke 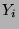 zunächst mit den
zunächst mit den 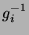 zu
zu 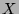 um.
Aus
um.
Aus 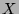 erzeugt man mit den
erzeugt man mit den 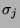 und
und 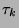 zwei Kopien von sich selbst. Diese kann mit den
zwei Kopien von sich selbst. Diese kann mit den  jeweils wieder
zu Kopien von
jeweils wieder
zu Kopien von 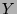 zurückbauen. Da in allen drei Schritten
Zerlegungen nur in endlich viele Teile vorkommen, genügt also
eine Zerlegung von
zurückbauen. Da in allen drei Schritten
Zerlegungen nur in endlich viele Teile vorkommen, genügt also
eine Zerlegung von 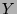 ebenfalls in endlich viele Teile, um das skizzierte
Programm mit entsprechenden Bewegungen durchzuführen.
ebenfalls in endlich viele Teile, um das skizzierte
Programm mit entsprechenden Bewegungen durchzuführen.
3.9 Eine paradoxe Zerlegung von
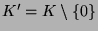
Die im letzten Abschnitt gefundene paradoxe Zerlegung von 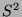 überträgt sich in offensichtlicher Weise auf
überträgt sich in offensichtlicher Weise auf
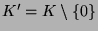 ,
(
,
( ), die Vollkugel ohne Mittelpunkt,
indem man an jedem Punkt
), die Vollkugel ohne Mittelpunkt,
indem man an jedem Punkt 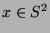 auf der Kugeloberfläche die Verbindungslinie zum Mittelpunkt der
Kugel anheftet. Die beteiligten Rotationen können direkt übernommen
werden.
auf der Kugeloberfläche die Verbindungslinie zum Mittelpunkt der
Kugel anheftet. Die beteiligten Rotationen können direkt übernommen
werden.
Etwas formaler sieht das so aus. Sei
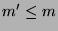 und
und 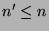 , die paradoxe Zerlegung von
, die paradoxe Zerlegung von 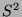 .
Für eine beliebige Teilmenge
.
Für eine beliebige Teilmenge
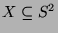 der Sphäre sei
der Sphäre sei 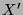 die Menge
aller
die Menge
aller
 ,
,
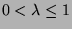 ,
, 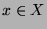 , also
die Menge aller Verbindungspunkte zwischen dem Mittelpunkt (exklusive)
und Punkten aus
, also
die Menge aller Verbindungspunkte zwischen dem Mittelpunkt (exklusive)
und Punkten aus 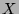 (inklusive). Dann ist
(inklusive). Dann ist
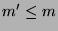 und
und 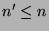 , die gesuchte paradoxe Zerlegung von
, die gesuchte paradoxe Zerlegung von 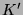 .
.
3.10 Vollendung des Beweises
Nach denselben Überlegungen wie in 3.8 genügt es
auch hier, wenn wir  zeigen.
Dabei beziehen wir uns wieder auf die Paradoxien des Unendlichen,
insbesondere jene aus 2.11. Diese besagt, dass die Kreislinie
zerlegungsäquivalent zur Kreislinie mit einem fehlenden Punkt ist.
Wir zerlegen daher
zeigen.
Dabei beziehen wir uns wieder auf die Paradoxien des Unendlichen,
insbesondere jene aus 2.11. Diese besagt, dass die Kreislinie
zerlegungsäquivalent zur Kreislinie mit einem fehlenden Punkt ist.
Wir zerlegen daher 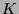 in irgendeine Kreislinie,
welche durch den Mittelpunkt verläuft, und den Rest. Diesen
Rest lassen wir unverändert. Die Kreislinie bleibt zerlegungsäquivalent,
wenn wir einen Punkt herausnehmen. Also gilt tasächlich
in irgendeine Kreislinie,
welche durch den Mittelpunkt verläuft, und den Rest. Diesen
Rest lassen wir unverändert. Die Kreislinie bleibt zerlegungsäquivalent,
wenn wir einen Punkt herausnehmen. Also gilt tasächlich
 , und der Beweis des PvBT ist erbracht.
(Man beachte, dass bei der Rotation der verwendeten Kreislinie
eine Rotation im Spiel ist, deren Achse nicht durch den Ursprung geht.)
, und der Beweis des PvBT ist erbracht.
(Man beachte, dass bei der Rotation der verwendeten Kreislinie
eine Rotation im Spiel ist, deren Achse nicht durch den Ursprung geht.)
4 Was lernen wir aus dem PvBT?
4.1 Nichtexistenz von Maßen
Die wichtigste Konsequenz des PvBT besteht in der Einsicht,
dass nicht allen Teilmengen von
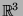 sinnvoll ein Volumen
zugewiesen werden kann.
Dabei verstehen wir unter sinnvoll, dass wenigstens
die Eigenschaften Positivität (
sinnvoll ein Volumen
zugewiesen werden kann.
Dabei verstehen wir unter sinnvoll, dass wenigstens
die Eigenschaften Positivität (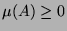 ,
,
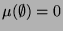 ),
Additivität (
),
Additivität (
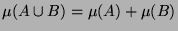 sofern
sofern
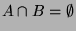 ),
Bewegungsinvarianz (
),
Bewegungsinvarianz (
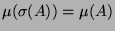 für Bewegungen
für Bewegungen
 und Normierung (
und Normierung (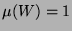 ,
, 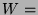 Einheitswürfel)
erfüllt sein sollen, so ist das PvBT der schlagende Beweis dafür,
dass unseren Wünschen Grenzen gesetzt sind.
Einheitswürfel)
erfüllt sein sollen, so ist das PvBT der schlagende Beweis dafür,
dass unseren Wünschen Grenzen gesetzt sind.
Wir gehen von einer beliebigen Kugel  mit positivem und
endlichem Radius aus. Ist
mit positivem und
endlichem Radius aus. Ist 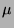 ein normiertes Maß, so hat
ein normiertes Maß, so hat
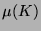 einen positiven und endlichen Wert.
Wir betrachten eine paradoxe Zerlegung
einen positiven und endlichen Wert.
Wir betrachten eine paradoxe Zerlegung
wie sie laut PvBT existiert. Wir nehmen an, den involvierten Mengen seien
in bewegungsinvarianter Weise Volumina
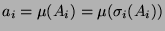 und
und
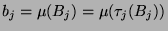 zugeordnet. Sei
zugeordnet. Sei
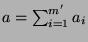 und
und
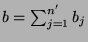 ,
dann führt die Additivität von
,
dann führt die Additivität von  einerseits zu
einerseits zu
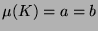 , andererseits wegen
, andererseits wegen  zu
zu
Damit kann 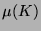 nur die Werte
nur die Werte 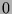 oder
oder 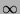 annehmen,
was aber zur Normierungsbedingung im Widerspruch steht.
Damit erweisen sich die Volumszahlen für die
annehmen,
was aber zur Normierungsbedingung im Widerspruch steht.
Damit erweisen sich die Volumszahlen für die 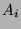 und
und 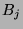 als widersprüchlich. Es kann also kein additives und bewegungsinvariantes
Maß im
als widersprüchlich. Es kann also kein additives und bewegungsinvariantes
Maß im
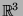 geben, welches für alle Teilmengen definiert ist.
geben, welches für alle Teilmengen definiert ist.
Man beachte, dass diese Konsequenz des PvBT insofern stärker ist als
das Vitalische Argument (vgl. [V]) für die Existenz nicht Lebesgue-messbarer
Mengen in 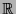 , als das PvBT nicht nur
, als das PvBT nicht nur  -additive
(d.h. abzählbar additive), sondern auch endliche
additive Maße ausschließt.
-additive
(d.h. abzählbar additive), sondern auch endliche
additive Maße ausschließt.
(Das Argument von Vitali lässt sich transparenter für die Kreislinie 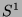 statt für das Einheitsintervall
statt für das Einheitsintervall
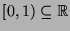 formulieren
und lautet folgendermaßen:
Auf
formulieren
und lautet folgendermaßen:
Auf 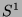 betrachte man die abzählbare Gruppe
betrachte man die abzählbare Gruppe  der Drehungen
um rationale Bruchteile
der Drehungen
um rationale Bruchteile 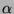 der vollen Rotation um
der vollen Rotation um 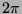 .
Bezüglich
.
Bezüglich 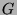 zerfällt
zerfällt 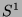 in Orbits
in Orbits  . Aus jedem Orbit wählt man einen
Punkt
. Aus jedem Orbit wählt man einen
Punkt 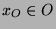 aus. Sei
aus. Sei 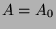 die Auswahlmenge aller
die Auswahlmenge aller
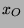 und
und 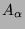 ,
,
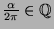 , das Bild von
, das Bild von 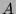 unter der Drehung um
unter der Drehung um 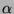 .
Dann bilden diese
.
Dann bilden diese 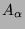 eine abzählbare Partition von
eine abzählbare Partition von 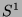 in
bewegungsgleiche Kopien von
in
bewegungsgleiche Kopien von 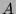 . Wäre
. Wäre 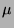 ein abzählbar additives
und drehinvariantes Maß auf
ein abzählbar additives
und drehinvariantes Maß auf 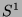 , so sind zwei Fälle zu unterscheiden.
, so sind zwei Fälle zu unterscheiden.
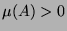 impliziert
impliziert
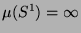 ,
, 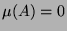 impliziert
impliziert
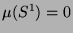 .
. 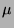 kann also in keinem Fall zu
kann also in keinem Fall zu 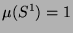 normiert werden.)
normiert werden.)
Notwendig für das stärkere PvBT war, dass im
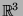 auch nicht kommutierende
Bewegungen auftreten, was bei den Translationen in
auch nicht kommutierende
Bewegungen auftreten, was bei den Translationen in 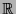 oder Drehungen von
oder Drehungen von
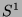 nicht der Fall ist.
nicht der Fall ist.
Tatsächlich zeigt eine allgemeinere Theorie paradoxer Zerlegungen, dass
die wichtige Rolle, welche in unserem Beweis die (hochgradig
nichtkommutative) von zwei Elementen frei erzeugte Gruppe spielt,
nicht zufällig ist, sondern im Wesen (gewisser) paradoxer Zerlegungen
liegt.
Hier sei noch der fundamentale Satz von Tarski (vgl. [T])
erwähnt, welcher besagt, dass
immer, wenn paradoxe Zerlegungen nicht existieren, nichttriviale endlich
additive Maße konstruiert werden können. Der Beweis dafür würde den hier
gegebenen Rahmen allerdings sprengen.
4.2 Bis 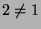 zählen und darüber hinaus
zählen und darüber hinaus
Mancher Leser mag versucht sein, das PvBT zur Formel  zu
komprimieren. Das ist aber nicht zulässig.
Die präzise Formulierung des PvBT (wie etwa in 1.3)
ist nämlich eine recht komplizierte Aussage,
in der Begriffe wie Punkte, Bewegungen, Drehungen, Teilmengen
etc. vorkommen. Es wurde aber nirgends die Gleichheit
zu
komprimieren. Das ist aber nicht zulässig.
Die präzise Formulierung des PvBT (wie etwa in 1.3)
ist nämlich eine recht komplizierte Aussage,
in der Begriffe wie Punkte, Bewegungen, Drehungen, Teilmengen
etc. vorkommen. Es wurde aber nirgends die Gleichheit 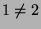 behauptet.
Was hätte ein Beweis der Implikation
behauptet.
Was hätte ein Beweis der Implikation
 für Konsequenzen?
für Konsequenzen?
Glücklicherweise ist die Mengenlehre so konstruiert, dass mit ihren
Mitteln der Satz 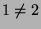 leicht bewiesen werden kann
(vgl. auch nächster Abschnitt). Weniger leicht, aber dennoch
schlüssig war der (stark mengentheoretisch geprägte) Beweis des PvBT.
Wäre auch die Implikation
leicht bewiesen werden kann
(vgl. auch nächster Abschnitt). Weniger leicht, aber dennoch
schlüssig war der (stark mengentheoretisch geprägte) Beweis des PvBT.
Wäre auch die Implikation
 beweisbar,
so hätten wir neben
beweisbar,
so hätten wir neben 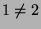 auch den Satz
auch den Satz  , was einen Widerspruch
bedeutete. Nach dem logischen Prinzip ex falso quodlibet
folgt aus einem Widerspruch aber Beliebiges. Also wäre jede
auch noch so absurde Aussage, welche sich überhaupt nur sinnvoll
mit den vogegebenen sprachlichen Mitteln (z.B. denen der Mengenlehre)
formulieren lässt, beweisbar. Damit wäre aber das übliche
mathematische System in seiner anerkannten Form unbrauchbar.
, was einen Widerspruch
bedeutete. Nach dem logischen Prinzip ex falso quodlibet
folgt aus einem Widerspruch aber Beliebiges. Also wäre jede
auch noch so absurde Aussage, welche sich überhaupt nur sinnvoll
mit den vogegebenen sprachlichen Mitteln (z.B. denen der Mengenlehre)
formulieren lässt, beweisbar. Damit wäre aber das übliche
mathematische System in seiner anerkannten Form unbrauchbar.
Da wir das System nicht grundlegend umstellen wollen, hoffen
wir nicht, dass
 bewiesen werden kann.
Eine Konsequenz des Unvollständigkeitssatzes von Gödel besteht
darin, dass es mit den Mitteln einer widerspruchsfreien
mathematischen Theorie nicht möglich ist, ihre eigene
Widerspruchsfreiheit zu beweisen. In diesem Sinne müssen
wir uns also mit der Hoffnung begnügen, dass wir nicht
zu Widersprüchen gelangen. Gewissheit gibt es nicht, es sei denn
wir lassen wesentlich stärkere Mittel zu. Diese bestünden aber in
mathematischen Annahmen, die nicht mehr Rechtfertigung
besitzen als die schlichte Zuversicht, dass die üblichen Voraussetzungen
(die mengentheoretischen Axiome, siehe
auch 4.4) widerspruchsfrei sind.
bewiesen werden kann.
Eine Konsequenz des Unvollständigkeitssatzes von Gödel besteht
darin, dass es mit den Mitteln einer widerspruchsfreien
mathematischen Theorie nicht möglich ist, ihre eigene
Widerspruchsfreiheit zu beweisen. In diesem Sinne müssen
wir uns also mit der Hoffnung begnügen, dass wir nicht
zu Widersprüchen gelangen. Gewissheit gibt es nicht, es sei denn
wir lassen wesentlich stärkere Mittel zu. Diese bestünden aber in
mathematischen Annahmen, die nicht mehr Rechtfertigung
besitzen als die schlichte Zuversicht, dass die üblichen Voraussetzungen
(die mengentheoretischen Axiome, siehe
auch 4.4) widerspruchsfrei sind.
In den obigen Erörterungen ist die Frage nach einem
mengentheoretischen Beweis für 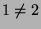 aufgetaucht.
Um einen solchen zu führen, müssen die Objekte 1 und 2 definiert
sein. In der mengentheoretisch fundierten Mathematik hat es sich als
naheliegend und praktisch
erwiesen, die natürlichen Zahlen so zu definieren,
dass jedes
aufgetaucht.
Um einen solchen zu führen, müssen die Objekte 1 und 2 definiert
sein. In der mengentheoretisch fundierten Mathematik hat es sich als
naheliegend und praktisch
erwiesen, die natürlichen Zahlen so zu definieren,
dass jedes 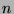 gleich der Menge seiner Vorgänger ist.
(Vor allem in Hinblick auf unendliche Ordinal- und Kardinalzahlen
erweist sich dieser Zugang zusammen mit dem zum Auswahlaxiom
äquivalenten Wohlordnungssatz als sehr mächtig.)
Damit ergibt sich
gleich der Menge seiner Vorgänger ist.
(Vor allem in Hinblick auf unendliche Ordinal- und Kardinalzahlen
erweist sich dieser Zugang zusammen mit dem zum Auswahlaxiom
äquivalenten Wohlordnungssatz als sehr mächtig.)
Damit ergibt sich 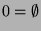 als leere Menge,
als leere Menge,
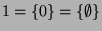 und
und
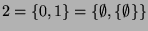 . Wäre
. Wäre  ,
so müssten die entsprechenden Mengen genau dieselben Elemente
besitzen. Insbesondere müsste das Element
,
so müssten die entsprechenden Mengen genau dieselben Elemente
besitzen. Insbesondere müsste das Element
 auch in 1 selbst enthalten sein. 1 enthält nur das Element
auch in 1 selbst enthalten sein. 1 enthält nur das Element 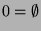 ,
also folgt
,
also folgt
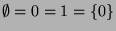 , d.h.
, d.h.
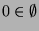 .
Die leere Menge
.
Die leere Menge 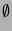 enthält definitionsgemäß aber keine
Elemente, Widerspruch.
enthält definitionsgemäß aber keine
Elemente, Widerspruch.
Vermutlich wird dieser Beweis als nicht sehr befriedigend empfunden,
weil alles von einer willkürlichen Definition der natürlichen Zahlen
abhängt. Tatsächlich gibt es hieraus einen Ausweg,
wenn man darauf verzichtet, die natürlichen Zahlen als fest definierte
Objekte aufzufassen:
Wir versuchen nicht, die Zahlen
 selbst zu definieren,
sondern lediglich festzulegen, was es bedeutet, wenn wir sagen:
Es gibt genau
selbst zu definieren,
sondern lediglich festzulegen, was es bedeutet, wenn wir sagen:
Es gibt genau
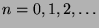 Objekte mit der Eigenschaft
Objekte mit der Eigenschaft 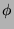 .
(Wir schreiben
.
(Wir schreiben 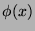 , falls
, falls  die Eigenschaft
die Eigenschaft 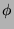 besitzt.)
Für
besitzt.)
Für  genügt es zu sagen, es gibt keine solchen Objekte.
Für
genügt es zu sagen, es gibt keine solchen Objekte.
Für  : Es gibt ein
: Es gibt ein 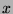 mit
mit 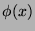 , und für alle
, und für alle 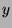 mit
mit
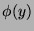 folgt
folgt 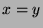 . Für
. Für  : Es gibt Elemente
: Es gibt Elemente 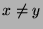 mit
mit 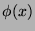 und
und 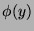 , und für jedes
, und für jedes 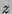 mit
mit 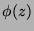 folgt
folgt
 oder
oder 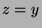 . (Es ist klar wie dies auf höhere Werte von
. (Es ist klar wie dies auf höhere Werte von  übertragen werden kann.) Das Wesentliche bei diesen Formulierungen ist,
dass nur rein logische Sprachelemente wie Negation, Folgerung,
die logischen Quantoren für alle und es gibt etc. vorgekommen sind
sowie die Identität
übertragen werden kann.) Das Wesentliche bei diesen Formulierungen ist,
dass nur rein logische Sprachelemente wie Negation, Folgerung,
die logischen Quantoren für alle und es gibt etc. vorgekommen sind
sowie die Identität  . Damit ist alles zurückgeführt auf die
fundamentale Frage, ob zwei Objekte identisch sind oder nicht.
. Damit ist alles zurückgeführt auf die
fundamentale Frage, ob zwei Objekte identisch sind oder nicht.
Man beachte, dass mit dieser Methode für jede einzelne natürliche
Zahl 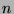 auf rein logischem Wege definiert werden kann,
wann die Anzahl gewisser Objekte
auf rein logischem Wege definiert werden kann,
wann die Anzahl gewisser Objekte 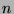 ist. Nicht jedoch
kann damit
ist. Nicht jedoch
kann damit 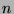 , geschweige denn so etwas wie die Menge aller natürlichen
Zahlen (aktual unendlich) als eigenständiges Objekt definiert werden.
, geschweige denn so etwas wie die Menge aller natürlichen
Zahlen (aktual unendlich) als eigenständiges Objekt definiert werden.
4.3 Der schwierige Begriff des Maßes
Wie geht der Mathematiker an die Aufgabe des Messens heran?
Der Erfolg seiner Disziplin hängt nicht nur von der strengen
Schlüssigkeit seiner Beweise ab, sondern, damit diese überhaupt erst
einen Sinn haben, von der klaren Definition seiner Objekte.
Will er das Volumen (Maß)
eines gegebenen geometrischen Körpers bestimmen,
so muss er zunächst einmal definieren, was er unter
geometrischem Körper und Volumen überhaupt versteht.
Dabei hat die Definition anders als in der Physik zu erfolgen
(vgl. 4.5).
Die mathematisch erfolgreichste Antwort auf die Frage, was ein Maß sei,
gibt die Mengenlehre.
Eines ihrer wesentlichen Merkmale ist, dass all ihre Objekte als
Mengen gedeutet werden. Tatsächlich haben wir ja auch die Kugel 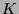 ,
um deren Zerlegung es im PvBT gegangen ist, als Menge von Punkten
im Raum aufgefasst. (Wie diese Punkte und ihre Koordinaten selbst
wiederum als Mengen gedeutet werden können,
spielt in unserem Kontext keine bedeutende Rolle, wir gehen daher nicht
näher darauf ein. Immerhin haben wir in 4.2
kurz angedeutet, wie man natürliche Zahlen als Mengen interpretieren kann.)
,
um deren Zerlegung es im PvBT gegangen ist, als Menge von Punkten
im Raum aufgefasst. (Wie diese Punkte und ihre Koordinaten selbst
wiederum als Mengen gedeutet werden können,
spielt in unserem Kontext keine bedeutende Rolle, wir gehen daher nicht
näher darauf ein. Immerhin haben wir in 4.2
kurz angedeutet, wie man natürliche Zahlen als Mengen interpretieren kann.)
Das Volumsmaß ist also mathematisch gesehen eine Abbildung 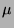 ,
welche gewissen Teilmengen
,
welche gewissen Teilmengen
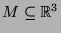 des Raumes
(insbesondere Würfeln, Kugeln etc.) eine reelle Maßzahl
des Raumes
(insbesondere Würfeln, Kugeln etc.) eine reelle Maßzahl 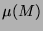 (oder auch
(oder auch  ) zuordnet.
Messen im mathematischen Sinn hat daher zumindest zwei Aspekte:
) zuordnet.
Messen im mathematischen Sinn hat daher zumindest zwei Aspekte:
- Definition der Abbildung
- Berechnung der Werte der Abbildung für spezielle Körper (Mengen)
Für den Ingenieur ist der zweite Punkt der spannendere, für den
Mathematiker eher der erste; auch wenn er die wichtige Aufgabe hat,
Berechnungsmethoden für den Ingenieur zu entwickeln.
Da sich der Artikel [We] in diesem Band viel ausführlicher
mit Inhalt und Maß auseinandersetzt, begnügen wir uns hier mit
kurzen Andeutungen. Bei der Definition der Werte 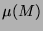 beginnt man
zunächst zum Beispiel mit der Forderung
beginnt man
zunächst zum Beispiel mit der Forderung 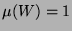 für den Einheitswürfel
für den Einheitswürfel 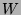 .
Dieser Wert muss definiert werden, er kann nicht aus physikalischen
Sachverhalten abgeleitet werden.
.
Dieser Wert muss definiert werden, er kann nicht aus physikalischen
Sachverhalten abgeleitet werden.
Wie auch schon in Abschnitt 4.1 erwähnt,
wünscht man sich von 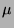 außerdem gewisse Eigenschaften wie
Positivität
außerdem gewisse Eigenschaften wie
Positivität 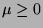 ,
,
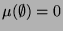 und Additivität, d.h.
und Additivität, d.h.
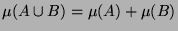 für
für
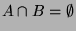 .
Entscheidend sind im
.
Entscheidend sind im
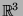 (wie in allen euklidischen Räumen
oder allgemeiner in Gruppen) auch Invarianzen
der Form
(wie in allen euklidischen Räumen
oder allgemeiner in Gruppen) auch Invarianzen
der Form
 für Translationen oder beliebige
Bewegungen
für Translationen oder beliebige
Bewegungen  . Im Beweis des PvBT haben solche Abbildungen
. Im Beweis des PvBT haben solche Abbildungen
 tatsächlich eine wesentliche Rolle gespielt.
tatsächlich eine wesentliche Rolle gespielt.
Aus den drei Bedingungen Additivität, Bewegungsinvarianz und Normierung
folgt vielerlei. So ergibt sich, dass der Einheitswürfel
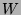 in acht Teilwürfel
in acht Teilwürfel 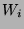 mit halber Seitenlänge zerfällt, deren Maß wegen
der Translationsinvarianz von
mit halber Seitenlänge zerfällt, deren Maß wegen
der Translationsinvarianz von 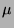 untereinander gleich und deren Summe
wegen der Additivität gerade
untereinander gleich und deren Summe
wegen der Additivität gerade 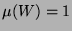 sein muss, also
sein muss, also
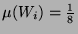 .
Ähnlich ergibt sich eindeutig das Volumen noch kleinerer Würfel.
Diese wiederum können verwendet werden, um Kugeln und viele andere Körper
.
Ähnlich ergibt sich eindeutig das Volumen noch kleinerer Würfel.
Diese wiederum können verwendet werden, um Kugeln und viele andere Körper
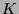 mit beliebig kleinem Fehler von innen zu füllen oder von außen zu
umschreiben. Das Volumen
mit beliebig kleinem Fehler von innen zu füllen oder von außen zu
umschreiben. Das Volumen 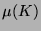 des Körpers muss wegen Additivität und
Positivität von
des Körpers muss wegen Additivität und
Positivität von 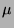 zwischen diesen beiden Approximationen liegen;
also etwa
zwischen diesen beiden Approximationen liegen;
also etwa
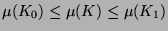 , wenn
, wenn  die innere und
die innere und  die äußere Approximation von
die äußere Approximation von 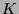 bezeichnet.
Zeigt man, dass
bezeichnet.
Zeigt man, dass 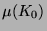 und
und 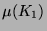 beliebig nahe
beisammen liegen können, bleib für
beliebig nahe
beisammen liegen können, bleib für 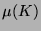 nur ein einziger möglicher
Wert dazwischen. Im Falle einer Kugel
nur ein einziger möglicher
Wert dazwischen. Im Falle einer Kugel 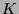 mit Radius
mit Radius 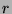 kann man
dann die bekannte Formel
kann man
dann die bekannte Formel
 beweisen.
(Das ist aber gar nicht so trivial!)
beweisen.
(Das ist aber gar nicht so trivial!)
Aus unseren Überlegungen folgt, dass, sofern es überhaupt eine sinnvolle
Möglichkeit gibt, Kugeln etc. ein Volumen zuzuweisen, dieses
aufgrund unserer Forderungen an 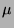 eindeutig
bestimmt ist. Wir müssen hier auf den zwar nicht
schwierigen, aber doch einigermaßen langwierigen Beweis verzichten,
dass diese Zuweisung auch wirklich
möglich ist. Das heißt, dass die Forderungen, die wir an
eindeutig
bestimmt ist. Wir müssen hier auf den zwar nicht
schwierigen, aber doch einigermaßen langwierigen Beweis verzichten,
dass diese Zuweisung auch wirklich
möglich ist. Das heißt, dass die Forderungen, die wir an 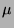 gestellt
haben, nicht zu Widersprüchen führen.
gestellt
haben, nicht zu Widersprüchen führen.
Man sieht leicht, dass sich mit den skizzierten Methoden nicht für alle
Teilmengen 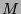 von
von
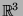 der Wert
der Wert 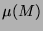 eindeutig ergibt.
Das klassische Beispiel hierzu ist die Menge der Punkte im
Einheitswürfel
eindeutig ergibt.
Das klassische Beispiel hierzu ist die Menge der Punkte im
Einheitswürfel 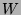 mit rationalen Koordinaten. Einerseits hat kein
noch so kleiner Würfel mit positivem Volumen darin Platz.
Also liefert die innere Approximation den Wert 0. Umgekehrt muss jede
endliche Überdeckung von
mit rationalen Koordinaten. Einerseits hat kein
noch so kleiner Würfel mit positivem Volumen darin Platz.
Also liefert die innere Approximation den Wert 0. Umgekehrt muss jede
endliche Überdeckung von 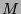 mit Würfeln bereits ganz
mit Würfeln bereits ganz 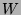 überdecken,
als äußere Approximation also mindestens
überdecken,
als äußere Approximation also mindestens 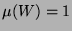 liefern.
Damit bleibt zwischen 0 und 1
eine Lücke der Unbestimmtheit übrig. Diese kann bei diesem
liefern.
Damit bleibt zwischen 0 und 1
eine Lücke der Unbestimmtheit übrig. Diese kann bei diesem
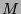 überbrückt werden, wenn man die Additivität von
überbrückt werden, wenn man die Additivität von 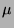 zur
zur
 -Additivität verschärft. Man argumentiert:
-Additivität verschärft. Man argumentiert: 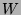 enthält nur
abzählbar viele Punkte, jeder davon hat Maß 0, ihre abzählbare Summe
soll sich daher auch nur zu 0 aufaddieren. Man erhält also
enthält nur
abzählbar viele Punkte, jeder davon hat Maß 0, ihre abzählbare Summe
soll sich daher auch nur zu 0 aufaddieren. Man erhält also 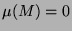 .
Dieser Zugang reflektiert die Vorstellung, dass abzählbare
Mengen im Vergleich zu überabzählbaren verschwindend klein sind.
Der Nachweis für die Existenz eines solchen
.
Dieser Zugang reflektiert die Vorstellung, dass abzählbare
Mengen im Vergleich zu überabzählbaren verschwindend klein sind.
Der Nachweis für die Existenz eines solchen  -additiven
Maßes zeigt natürlich mehr als jener für die endliche
Additivität, ist aber auch dementsprechend schwieriger.
Aus 4.1 wissen wir dass bezüglich eines
-additiven
Maßes zeigt natürlich mehr als jener für die endliche
Additivität, ist aber auch dementsprechend schwieriger.
Aus 4.1 wissen wir dass bezüglich eines  -additiven
Maßes nicht nur in
-additiven
Maßes nicht nur in
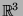 , sondern schon in
, sondern schon in 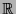 nichtmessbare
Mengen existieren. Deshalb sind die grundsätzlichen
Schwierigkeiten durch Ausweitung auf
nichtmessbare
Mengen existieren. Deshalb sind die grundsätzlichen
Schwierigkeiten durch Ausweitung auf  -Additivität
nur verschoben, nicht aber aufgehoben.
-Additivität
nur verschoben, nicht aber aufgehoben.
Als Konsequenz unserer Überlegungen erkennen wir, dass
Zählen und Messen
begrifflich sehr unterschiedliche Operationen sind.
Bestenfalls kann das Zählen als sehr einfacher Spezialfall
des Messens interpretiert werden, wo als Maßzahlen nur die
natürlichen auftreten und als invariante Transformationen
beliebige bijektive (umkehrbar eindeutige) Abbildungen zugelassen sind.
Wir fassen einige Unterschiede zusammen:
- Der Maßstab des Zählens sind die natürlichen Zahlen,
der des Messens die reellen.
- Jede natürliche Zahl kann durch eine rein logische
Formel beschrieben werden, was bei reellen Zahlen
(z.B. schon aus Kardinalitätsgründen) nicht möglich ist.
- Das Zählen beruht nur auf der Identität
 als fundamentaler
logischer Relation, während beim Messen Transformationen
(Translationen, Bewegungen) als fundamentales Instrument
des Vergleichs benötigt werden.
als fundamentaler
logischer Relation, während beim Messen Transformationen
(Translationen, Bewegungen) als fundamentales Instrument
des Vergleichs benötigt werden.
- Die konzeptuelle Entwicklung der Maßtheorie ist ungleich
aufwendiger als die der Arithmetik natürlicher Zahlen.
- Die Anzahl
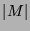 ist stets definiert (für unendliche
Mengen leisten die unendlichen Kardinalzahlen das Gewünschte),
während
ist stets definiert (für unendliche
Mengen leisten die unendlichen Kardinalzahlen das Gewünschte),
während 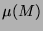 für besonders kompliziert gebaute Mengen
für besonders kompliziert gebaute Mengen 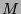 nicht sinnvoll zu definieren ist.
nicht sinnvoll zu definieren ist.
4.4 Das Auswahlaxiom
Es ist unvermeidlich, noch ein paar Bemerkungen über das Auswahlaxiom
(Axiom of Choice, AC) zu verlieren und über seine Rolle im Beweis des PvBT und
in verwandten Resultaten der Maßtheorie. Tatsächlich kann man zeigen,
dass ein Beweis des PvBT ohne Auswahlaxiom grundsätzlich unmöglich ist.
Lässt man eine Verletzung des Auswahlaxioms zu, so kann man nämlich, wie
Solovay in [So] gezeigt hat, widerspruchsfrei annehmen, dass alle Teilmengen
reeller Zahlen messbar sind. Allerdings liegt das daran,
dass man ohne Auswahlaxiom die nicht messbaren Mengen nicht finden kann
und nur deshalb auf keinen Widerspruch stößt.
Es wird oft nicht darauf hingewiesen, dass man statt des
Auswahlaxioms mit gleichem Recht auch andere Axiome der Mengenlehre
für das PvBT verantwortlich machen könnte. Ohne Potenzmengenaxiom
beispielsweise könnte man keine überabzählbaren Mengen konstruieren
(vgl. 2.7), also weder 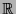 noch die Kugel.
Ohne Unendlichkeitsaxiom bliebe man sogar schon im Endlichen stecken.
Damit hätte man überhaupt sämtliche Paradoxien des Unendlichen verbannt.
Und auch das Vereinigungsmengenaxiom wird zur Konstruktion
wenigstens scheinbar großer Mengen herangezogen.
Trotzdem hat gerade das Auswahlaxiom vor allem zu Beginn des
20. Jahrhunderts so viele Diskussionen entfacht:
noch die Kugel.
Ohne Unendlichkeitsaxiom bliebe man sogar schon im Endlichen stecken.
Damit hätte man überhaupt sämtliche Paradoxien des Unendlichen verbannt.
Und auch das Vereinigungsmengenaxiom wird zur Konstruktion
wenigstens scheinbar großer Mengen herangezogen.
Trotzdem hat gerade das Auswahlaxiom vor allem zu Beginn des
20. Jahrhunderts so viele Diskussionen entfacht:
AC: Ist 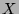 eine Menge von nichtleeren und paarweise disjunkten Mengen
eine Menge von nichtleeren und paarweise disjunkten Mengen
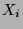 , so gibt es eine sogenannte Auswahlmenge
, so gibt es eine sogenannte Auswahlmenge 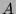 , welche aus jedem
, welche aus jedem
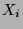 genau ein Element (einen Repräsentanten) enthält.
genau ein Element (einen Repräsentanten) enthält.
Wie kann eine so plausible Annahme auch heute noch manche Gemüter erhitzen?
Das erscheint sehr plausibel, dennoch haben die Diskussionen darüber
Tradition. Im Zusammenhang mit dem PvBT, in dessen Beweis wir AC
ja verwendet haben (nämlich in 3.5), könnte man zunächst einwenden,
dass die Aussage des PvBT zu paradox ist. Das hieße aber, den Standpunkt
(= Gesichtskreis vom Radius 0) einnehmen, dass nicht sein könne, was
nicht sein darf. Wir hoffen, dass der Leser den Beweis
- auch wenn er ihn vielleicht nicht in allen Details überprüft hat -
als überzeugend nachvollziehen konnte.
Eine eingehendere Analyse ist also gefragt.
Ein etwas subtilerer Einwand, der das Wesen des Auswahlaxioms
und auch des PvBT besser trifft, besteht in der Kritik, dass die Auswahlmenge
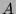 lediglich als existent gefordert wird, dass aber keine nähere
Beschreibung mitgeliefert wird. Andere Axiome der Mengenlehre,
die zum Beispiel die Existenz von Vereinigungs- oder Potenzmengen
sichern, scheinen diesen Mangel nicht zu haben.
lediglich als existent gefordert wird, dass aber keine nähere
Beschreibung mitgeliefert wird. Andere Axiome der Mengenlehre,
die zum Beispiel die Existenz von Vereinigungs- oder Potenzmengen
sichern, scheinen diesen Mangel nicht zu haben.
Hier wird aber die Auffassung vertreten, dass diese Unterschiede nur
gradueller Art sind. Mathematische Objekte (und vermutlich alle
Objekte unseres Denkens) sind stets mit dem erkenntnistheoretischen
Mangel behaftet, dass wir von ihnen nur gewisse Eigenschaften kennen
und nicht alle, geschweige denn das von Kant als unerkennbar
diagnostizierte Ding an sich. So wissen wir von der Auswahlmenge 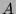 im Wesentlichen nur das, was uns das Auswahlaxiom liefert. Genauso wissen wir
durch Knochenfunde von Urmenschen auch nicht, in welcher
Sprache sie sich unterhalten haben. Dennoch zweifeln wir nicht an
ihrer prähistorischen Existenz.
im Wesentlichen nur das, was uns das Auswahlaxiom liefert. Genauso wissen wir
durch Knochenfunde von Urmenschen auch nicht, in welcher
Sprache sie sich unterhalten haben. Dennoch zweifeln wir nicht an
ihrer prähistorischen Existenz.
In mancherlei Hinsicht kann man die Rolle des Auswahlaxioms in der Mathematik
auch mit der des Teleskops in der Astronomie vergleichen: Man kann
wesentlich mehr damit sehen, auch wenn die betrachteten
Objekte dadurch im wörtlichen Sinn um nichts greifbarer werden.
Außerdem muss betont werden, dass sich die Mathematik
im Unterschied zur Paläoontologie oder auch zur Astronomie
grundsätzlich nur mit ideellen Objekten beschäftigt,
von denen nur gewisse Eigenschaften relevant sind.
Beispiel: Beim Begriff der Zahl 2 kommt es darauf an, dass sie z.B. der Summe  entspricht; wir kümmern uns aber nicht um ihre Farbe,
Laune, etc.
entspricht; wir kümmern uns aber nicht um ihre Farbe,
Laune, etc.
Angemessen gegenüber Auswahl- wie auch anderen Axiomen
der Mengenlehre oder Mathematik generell mag es daher sein,
wenn man sie als explizit formulierte Denkfreiheiten
ansieht, nicht jedoch als gratis Erkenntnisquelle für die
empirische Wirklichkeit. Der Gegenstand der Mathematik geht nämlich
über die Erfahrungswelt und sogar über den Bereich des
Vorstellbaren hinaus und erschließt sich die
schillernde Welt des Denkmöglichen. (In [M] ist der Mann mit dem
Möglichkeits- statt Wirklichkeitssinn nicht zufällig Mathematiker!)
Wer mathematische Axiome aus metaphysischen oder ideologischen Gründen
ablehnt, spricht also Denkverbote aus. Wer hingegen untersucht,
welche Ergebnisse auch ohne Verwendung gewisser Prämissen und Axiome
erzielbar sind und welche nicht, betreibt seriöse Mathematik,
möglicherweise auf allerhöchstem Niveau.
Das dies keine leeren Worte sind, lässt sich sogar durch mathematische
Ergebnisse belegen: Gödel zeigte, dass das Auswahlaxiom zu keinen
Widersprüchen führt (also denkbar ist), sofern nur die übrigen
und weit weniger diskutierten Axiome der gängigen Mengenlehre
widerspruchsfrei sind. Aber auch die Verletzung des Auswahlaxioms
ist widerspruchsfrei denkbar, wie später Cohen gezeigt hat. Damit liegt eines
der prominentesten Beispiele eines sogenannten Unabhängigkeitsresultats
vor.
Vollkommen analog dazu (auch was die Rollen von Gödel und Cohen
betrifft) ist die Situation hinsichtlich der sogenannten Kontinuumshypothese.
Hilbert hob sie im Jahre 1900 sogar als das erste
und fundamentalste der berühmten 23 Probleme hervor,
deren Beantwortung er als zentrale Aufgabe für das damals
bevorstehende 20. Jahrhundert betrachtete.
Die offene Frage lautet: Gibt es überabzählbare Mengen,
die echt kleiner als das Kontinuum sind? Auch diese Frage erwies sich als
mit den gängigen Axiomen der Mengenlehre nicht entscheidbar.
4.5 Mathematisches versus physikalisches Messen
Im Zusammenhang mit dem PvBT scheint es nicht unwesentlich,
den Unterschied zwischen mathematischen und physikalischen
Volumsbegriffen herauszuarbeiten. Dem mathematischen Zugang
war Abschnitt 4.3 gewidmet.
Doch was versteht der Physiker unter dem Volumen z.B. einer
Kugel? Der Leser möge innehalten und selbst nach einer Antwort suchen!
Eine physikalische Möglichkeit der Volumsmessung ist die folgende:
Man taucht den Körper in einen quaderförmigen Behälter mit Wasser,
dessen Grundfläche ein Quadrat mit Seitenlänge 1 ist, und
misst den Anstieg des Wasserspiegels.
Die Maßzahl dieses Anstiegs in Längeneinheiten stimmt dann mit der
Maßzahl des Volumens des Körpers in Volumseinheiten überein.
Dieses Verfahren führt die Messung eines Volumens auf die
einfachere Messung einer Länge zurück. Es
setzt allerdings voraus, dass das Wasser auf diese Art nicht
komprimiert wird, d.h. sein Volumen beibehält. Aber damit ist ja
auch bereits ein Volumsbegriff vorausgesetzt!
Die Katze beißt sich also in den Schwanz.
Aus der Sicht des Physikers ist das aber nicht so tragisch.
Entscheidend ist für ihn,
dass die Wiederholung des beschriebenen Messvorgangs
immer wieder zum selben Ergebnis führt. Damit ist ein praktikabler
Kontext hergestellt, in dem von einer physikalischen Größe
Volumen gesprochen werden kann. Dass das Experiment
tatsächlich immer dasselbe Ergebnis liefert, ist eine empirische
(aus der Erfahrung stammende) Tatsache, die durch widersprechende Erfahrungen
prinzipiell auch widerlegt werden könnte. Das entspricht exakt der
Popperschen Forderung nach Falsifizierbarkeit von Aussagen empirischer
Wissenschaften. Mathematische Aussagen sind aber von anderem
Charakter. Sie beschreiben das auf empirische Art nicht bestimmbare
Wesen von Begriffen, die vor allem in logischem Kontext
ihren Sinn entfalten.
Doch ist noch ein Wort zur physikalischen Längenmessung angebracht,
auf welche wir oben die Volumsmessung zurückgeführt haben.
Was tun wir denn, wenn wir eine Länge mit einem Maßstab messen?
Wir bewegen zuerst den Maßstab zum zu vermessenden Gegenstand
und führen dann einen Vergleich durch. Es wird also auch hier
eine (empirisch gerechtfertigte) Invarianz von Längenmaßen unter
Bewegungen vorausgesetzt. Man mache sich den Unterschied zu den
begrifflich bestimmten Invarianzen eines mathematischen
Längenbegriffs klar!
Dass diese Überlegungen keine müßigen Haarspaltereien sind, zeigt sich
in spektakulärer Weise in der empirisch mittlerweile in höchstem Maße
gesicherten Einsteinschen Relativitätstheorie.
Sie impliziert nämlich, dass genau die
unterstellten Invarianzen von Länge (und Zeit) verlorengehen, wenn sehr große
Geschwindigkeiten oder sehr starke Gravitationsfelder wirksam werden.
Dennoch steht das nicht im Widerspruch zur Mathematik.
Man muss nur eine kompliziertere Raumstruktur als Modell verwenden.
Bezeichnend ist, dass die wesentlichen Ideen dazu auf den Mathematiker
Riemann zurückgehen, der ungefähr ein halbes Jahrhundert
vor Einstein wirkte und (wie dieser übrigens auch)
seine Ideen seiner Phantasie und keinen empirischen Messdaten verdankte.
Die großen Unterschiede zwischen mathematischem (vgl. 4.3)
und physikalischem Messen lassen es nicht mehr verwunderlich erscheinen,
dass die Mathematik Denkbarkeiten eröffnet, die physikalisch nicht
realisierbar sind. Kritiker der Mathematik und insbesondere der
mengentheoretischen Grundlegung mögen einwenden, dass sie
unbrauchbare Modelle für die Welt liefere. Wir hingegen sehen
einen Erkenntnisfortschritt darin, dass durch Ausweitung des Bereichs
des Denkbaren (vgl. auch 4.4)
jener des Machbaren nicht nur von innen, sondern
auch von außen besser eingegrenzt und damit besser verstanden
werden kann.
4.6 Didaktische Konsequenzen
Im Hinblick auf den Unterricht in Schulen soll die vorliegende
Aufbereitung des PvBT belegen, dass die gleichzeitige
Umsetzung folgender Ziele möglich ist:
- Präsentation eines attraktiven Resultats: Etwas Spektakuläreres
als das PvBT gibt es in der Wissenschaft kaum.
- Vollständiger Beweis: Die mathematischen
Voraussetzungen für den präsentierten Beweis sollten schon zwei
Jahre vor der Matura vorhanden sein.
- Interessante inner- und außermathematische Querverbindungen:
Problematik des Maß- und Inhaltsbegriffs, Beziehungen
zwischen Mathematik und Physik, prinzipielle
Erkenntnisgrenzen etc.
- Auffächerung in viele Hilfsresultate, die auch für sich
interessant sind: Abzählbare und überabzählbare Mengen,
Darstellung von Drehungen durch Abbildungsgleichungen,
Gruppen allgemein und speziell die freie Gruppe etc.
Bei der didaktischen Aufbereitung anspruchsvoller mathematischer
Inhalte erscheinen für das Erreichen obiger Ziele
folgende Mittel als hilfreich:
- Entformalisierung, Ideen statt Kalküle:
Die mathematische Zeichensprache
hat ihre großen Meriten für den Fachmann und ist
aus einer fruchtbaren mathematischen Forschung
nicht wegzudenken. Will man bedeutende mathematische
Ideen hinter der Formelsprache verständlich machen,
wird dem in der Formelsprache
weniger Geübten das Verständnis wesentlich
leichter fallen, wenn die Sprachschwierigkeiten
möglichst reduziert werden. Außerdem stehen
auch für den mathematischen Forscher
in der Regel die Ideen im Mittelpunkt
und nicht die formalen Kalküle. Insbesondere bei
geometrischen Überlegungen wie dem PvBT leistet die
natürliche Sprache oft bessere Dienste als die formalisierte.
Auch Abbildungen, auf welche in diesem Text aus technischen
Gründen leider verzichtet werden musste,
spielen eine wichtige Rolle. Generell sind solche mathematischen
Inhalte besser vermittelbar, die auch ohne großen formalen
Aufwand verständlich gemacht werden können.
Leider hat diese Tatsache im Schulunterricht nicht
immer angemessene Berücksichtigung gefunden. (Warum?)
- Zerlegung in kleine Einheiten: Die allermeisten Schüler
(und nicht nur diese) werden durch allzu lange Schlussketten
überfordert. Deshalb scheint es ratsam, einzelnen Beweisschritten
den Charakter einer attraktiven und einprägsamen
Idee abzugewinnen und ihrer Behandlung
mehr Raum einzuräumen. Im Text wurde das dadurch hervorgehoben,
dass die beweistechnischen Kapitel 2 und 3
in relativ ausführliche Abschnitte gegliedert wurden, die
jeweils einem einzigen Hauptgedanken gewidmet sind.
- Der Weg ist das Ziel: Im Beweis des PvBT spielten abzählbare
und überabzählbare unendliche Mengen eine entscheidende Rolle.
Was spricht dagegen, diesen zentralen Aspekten der Mengenlehre
einige Zeit zu widmen? Nicht viel! Ähnliches gilt für die analytische
Beschreibung der Drehungen in 3.6 und 3.7.
Es wäre für den Unterricht doch bereichernd, die Behandlung linearer
Gleichungssysteme durch die geometrische Interpretation
als Abbildungen zu ergänzen. Auch die freie Gruppe lässt sich
in anderem Kontext (z.B. Wortproblem,
automatisches Beweisen, Gödelscher Satz) sinnvoll
als per se interessantes Objekt behandeln.
- Zentrale Beweisidee: Hat man einen wichtigen Satzes als
vordringliches Ziel vor Augen, so erweist sich statt einer
strikt linearen Abarbeitung des Beweises didaktisch ein anderer
Weg als zielführender, nämlich die Identifikation
und Hervorhebung einer oder weniger
entscheidenden Beweisideen als Ausgangspunkt. Im Falle des
PvBT bieten sich die paradoxe Zerlegung der freien Gruppe
(3.3) und die Aussicht auf Realisierung
mittels Drehungen an. Von hier ausgehend lassen sich
alle anderen Beweiselemente als sehr natürliche Schritte
leicht motivieren.
- Mut zur Subjektivität: Dieser Artikel will nicht jeden Methamatiklehrer
dazu überreden, das PvBT im Unterricht zu behandeln.
Übergeordnet ist das Anliegen, anhand eines Beispiels, welches dem
Autor sehr geeignet erscheint, zur Umsetzung ehrgeiziger Ziele
im Mathematikunterricht zu ermutigen. Die Schüler werden von
einem schwierigen Resultat, das mit Begeisterung behandelt wird,
mehr verstehen, als von einer flachen Trivialität, die nur aus
Pflichtgefühl und mit dementsprechender Langeweile vorgetragen wird.
Um von diesen allgemeinen Gedanken über den Mathematikunterricht nochmals
zum PvBT zurückzukehren, wollen wir mit der Empfehlung schließen,
die paradoxe Zerlegung einer Kugel aus Holz, Stein, Metall oder anderen
Materialien nicht im Werkunterricht zu versuchen.
-
- Ba-T
-
S. Banach und A. Tarski. Sur la decomposition des ensembles de
points en parties respectivement congruent.
Fund. Math. 6 (1924), 244-277.
- Bo
- B. Bolzano. Paradoxien des Unendlichen.
1851, Reclam, Leipzig.
- Ga
- Galileo. Dialogues Concerning Two New Sciences.
1914, Macmillan, New York. Übersetzung des Originaltextes von 1638.
- Go
- M. Goldstern. Mengenlehre: Hierarchie des Unendlichen.
Didaktikhefte, Österr. Math. Gesellschaft, Schriftenreihe zur
Didaktik der Mathematik der Höheren Schulen, Heft 32, 59-72.
- H
- F. Hausdorff. Bemerkungen über den Inhalt von Punktmengen.
Math. Ann. 75 (1914), 428-433.
- M
- R. Musil. Der Mann ohne Eigenschaften. Rowohlt.
- So
- R. M. Solovay. A model of set theory in which every
set of reals is Lebesgue measurable. Ann. Math. 92 (1970), 1-56.
- St
- K. Stromberg. The Banach-Tarski Paradox.
Amer. Math. Monthly 86 (1979), Nr.3, 151-161.
- T
- A. Tarski. Algebraische Fassung des Maßproblems.
Fund. Math. 31 (1938), 47-66.
- V
- G. Vitali. Sul problema della mesura dei gruppi
di punti in una retta. 1905, Bologna.
- Wa 1
- S. Wagon. Circle-squaring in the twentieth century.
Math. Intelligencer 3 (1980/81), Nr.4, 176-181.
- Wa 2
- S. Wagon. The Banach-Tarski Paradox.
Cambridge University Press 1985.
- We
- W. Wertz. Inhalt und Maß.
Didaktikhefte, Österr. Math. Gesellschaft, Schriftenreihe zur
Didaktik der Mathematik der Höheren Schulen, Heft 33.
Erstellt durch "LaTeX2html" am 10.Mai 2001
Zurück zu
Reinhard Winklers
Homepage